
【题目】如图:
(1)写出A、B、C三点的坐标;
(2)若△ABC各顶点的横坐标不变,纵坐标都乘以﹣1,请你在同一坐标系中描出对应的点A′、B′、C′,并依次连接这三个点,所得的△A′B′C′与原△ABC有怎样的位置关系;
(3)在②的基础上,纵坐标都不变,横坐标都乘以﹣1,在同一坐标系中描出对应的点A″、B″、C″,并依次连接这三个点,所得的△A″B″C″与原△ABC有怎样的位置关系.

【答案】(1)A(3,4)B(1,2)C(5,1)
(2)描点画图见解析,△A′B′C′与△ABC关于x轴对称;
(3)描点画图见解析,△A″B″C″与原△ABC关于原点对称.
【解析】
(1)根据各点坐标描出各点;
(2)将题目中各点横坐标不变纵坐标分别乘以﹣1,再描出各点连接各点;
(3)将题目中各点纵坐标不变横坐标分别乘以﹣1,再描出各点连接各点.
解:(1)根据各点的位置,各点坐标为:A(3,4)、B(1,2)、C(5,1);
(2)由(1)A(3,4)、B(1,2)、C(5,1),横坐标不变,纵坐标都乘以-1,得:A′(3,-4)、B′(1,-2)、C′(5,-1),△A′B′C′与△ABC关于x轴对称;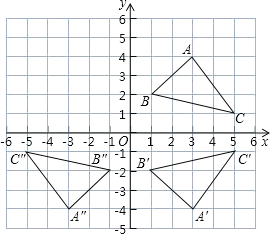
(3)A(3,4)、B(1,2)、C(5,1),纵坐标都不变,横坐标都乘以-1,得:A″(-3,4)、B″(-1,2)、C″(-5,1),则△A″B″C″与△ABC关于原点对称.


 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案科目:初中数学 来源: 题型:
【题目】某小学学生较多,为了便于学生尽快就餐,师生约定:早餐一人一份,一份两样,一样一个,食堂师傅在窗口随机发放(发放的食品价格一样),食堂在某天早餐提供了猪肉包、面包、鸡蛋、油饼四样食品.
(1)按约定,“小李同学在该天早餐得到两个油饼”是 事件;(可能,必然,不可能)
(2)请用列表或树状图的方法,求出小张同学该天早餐刚好得到猪肉包和油饼的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:四边形ABCD中,∠ABC=∠ADC=90°,AB=BC,连接BD.
(1)画出示意图;
(2)请问:DB平分∠ADC吗?请给出结论,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请阅读下列材料:
问题:如图1,点A,B在直线l的同侧,在直线l上找一点P,使得AP+BP的值最小.
小明的思路是:如图2所示,先作点A关于直线l的对称点A′,使点A′,B分别位于直线l的两侧,再连接A′B,根据“两点之间线段最短”可知A′B与直线l的交点P即为所求.
请你参考小明同学的思路,探究并解决下列问题:
(1)如图3,在图2的基础上,设AA'与直线l的交点为C,过点B作BD⊥l,垂足为D.若CP=1,AC=1,PD=2,直接写出AP+BP的值;
(2)将(1)中的条件“AC=1”去掉,换成“BD=4﹣AC”,其它条件不变,直接写出此时AP+BP的值;
(3)请结合图形,求![]() 的最小值.
的最小值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,规定把一个三角形先沿x轴翻折,再向右平移两个单位称为一次变换,如图,已知等边三角形ABC的顶点B、C的坐标分别是,(-1,-1),(-3,-1),把三角形ABC经过连续9次这样的变换得到三角形A’B’C’,则点A的对应点A’的坐标是_____

查看答案和解析>>
科目:初中数学 来源: 题型:
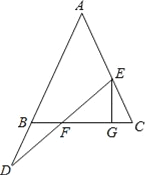
【题目】如图,在△ABC中,AB=AC,点E在线段AC上,D在AB的延长线上,连接DE交BC于F,过E作EG⊥BC于G.
(1)下列两个关系式:①DB=EC,②DF=EF,请你选择一个做为条件,另一个做为结论构成一个正确的命题,并给予证明.
你选择的条件是 ,结论是 .(只需填序号)
(2)在(1)的条件下,求证:FG=BC/2.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2016年3月国际风筝节期间,王大伯决定销售一批风筝,经市场调研:蝙蝠型风筝进价每个为10元,当售价每个为12元时,销售量为180个,若售价每提高1元,销售量就会减少10个,请回答以下问题:
(1)用表达式表示蝙蝠型风筝销售量y(个)与售价x(元)之间的函数关系(12≤x≤30);
(2)王大伯为了让利给顾客,并同时获得840元利润,售价应定为多少?
(3)当售价定为多少时,王大伯获得利润W最大,最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】【问题背景】
(1)如图1的图形我们把它称为“8字形”,请说明![]() ;
;

【简单应用】
(2)阅读下面的内容,并解决后面的问题:如图2, AP、CP分别平分∠BAD. ∠BCD,若∠ABC=36°,∠ADC=16°,求∠P的度数;

解:∵AP、CP分别平分∠BAD. ∠BCD
∴∠1=∠2,∠3=∠4
由(1)的结论得: ![]()
①+②,得2∠P+∠2+∠3=∠1+∠4+∠B+∠D
∴∠P =![]() (∠B+∠D)=26°.
(∠B+∠D)=26°.
【问题探究】如图3,直线AP平分∠BAD的外角∠FAD,CP平分∠BCD的外角∠BCE,若∠ABC=36°,∠ADC=16°,请猜想![]() 的度数,并说明理由.
的度数,并说明理由.

【拓展延伸】
① 在图4中,若设∠C=α,∠B=β,∠CAP=![]() ∠CAB,∠CDP=
∠CAB,∠CDP=![]() ∠CDB,试问∠P与∠C、∠B之间的数量关系为:________________(用α、β表示∠P),
∠CDB,试问∠P与∠C、∠B之间的数量关系为:________________(用α、β表示∠P),

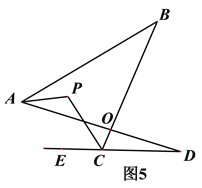
②在图5中,AP平分∠BAD,CP平分∠BCD的外角∠BCE,猜想∠P与∠B、∠D的关系,直接写出结论______________________
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】由于受到手机更新换代的影响,某手机店经销的华为P10 plus手机四月售价比三月每台降价500元.如果卖出相同数量的华为P10 plus手机,那么三月销售额为9万元,四月销售额只有8万元.
(1)三月华为P10 plus手机每台售价为多少元?
(2)为了提高利润,该店计划五月购进华为P20 pro手机销售,已知华为P10 plus每台进价为3500元,华为P20 pro每台进价为4000元,预计用不多于7.6万元且不少于7.4万元的资金购进这两种手机共20台,请问有几种进货方案?
(3)该店计划六月对华为P10 plus的尾货进行销售,决定在四月售价基础上每售出一台华为P10 plus手机再返还顾客现金![]() 元,而华为P20 pro按销售价4400元销售,如要使(2)中所有方案获利相同,
元,而华为P20 pro按销售价4400元销售,如要使(2)中所有方案获利相同,![]() 应取何值?
应取何值?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com