
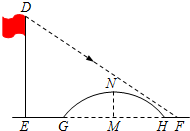
 如图所示,该小组发现8米高旗杆DE的影子EF落在了包含一圆弧型小桥在内的路上,于是他们开展了测算小桥所在图的半径的活动.小刚身高1.6米,测得其影长为2.4米,同时测得EG的长为3米,HF的长为1米,测得拱高(弧GH的中点到弦GH的距离,即MN的长)为2米,则小桥所在圆的半径
如图所示,该小组发现8米高旗杆DE的影子EF落在了包含一圆弧型小桥在内的路上,于是他们开展了测算小桥所在图的半径的活动.小刚身高1.6米,测得其影长为2.4米,同时测得EG的长为3米,HF的长为1米,测得拱高(弧GH的中点到弦GH的距离,即MN的长)为2米,则小桥所在圆的半径| DE |
| EF |
| 1.6 |
| 2.4 |
| 1 |
| 2 |
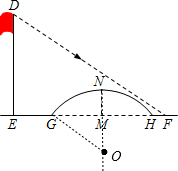 小桥所在圆的圆心为点O,连结OG,设⊙O的半径为Rm,如图,
小桥所在圆的圆心为点O,连结OG,设⊙O的半径为Rm,如图,| DE |
| EF |
| 1.6 |
| 2.4 |
| 8 |
| 3+GH+1 |
| 1.6 |
| 2.4 |
| 1 |
| 2 |


 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案科目:初中数学 来源: 题型:
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 5 |
| 3 |
| 4 |
| 3 |
| 4 |
| 7 |
| 8 |
| 5 |
| 12 |
| 1 |
| 2 |
| 2 |
| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
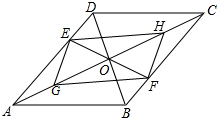 如图,?ABCD的对角线AC、BD交于点O,EF过点O交AD于E,交BC于F,G、H都是对角线AC上的点,且AG:OA=1:3,CH:OC=1:3,求证:四边形EGFH是平行四边形.
如图,?ABCD的对角线AC、BD交于点O,EF过点O交AD于E,交BC于F,G、H都是对角线AC上的点,且AG:OA=1:3,CH:OC=1:3,求证:四边形EGFH是平行四边形.查看答案和解析>>
科目:初中数学 来源: 题型:
 一部分同学围在一起做“传数”游戏,我们把某同学传给后面的同学的数称为该同学的“传数”.游戏规则是:同学1心里先想好一个数,将这个数乘以2再加1后传给同学2,同学2把同学1告诉他的数除以2再减
一部分同学围在一起做“传数”游戏,我们把某同学传给后面的同学的数称为该同学的“传数”.游戏规则是:同学1心里先想好一个数,将这个数乘以2再加1后传给同学2,同学2把同学1告诉他的数除以2再减| 1 |
| 2 |
| 1 |
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
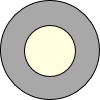 如图,在一个半径为20厘米的圆面上,从中心挖去一个半径为x厘米的圆面,当挖去的圆的半径由小变大时,剩下的圆环面积也随之变化
如图,在一个半径为20厘米的圆面上,从中心挖去一个半径为x厘米的圆面,当挖去的圆的半径由小变大时,剩下的圆环面积也随之变化查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com