
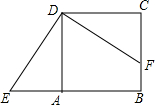
 如图,正方形ABCD中,点F在边BC上,E在边BA的延长线上,△DCF按顺时针方向旋转后恰好与△DAE重合,若AE=3,BF=2,则四边形BFDE的面积是25.
如图,正方形ABCD中,点F在边BC上,E在边BA的延长线上,△DCF按顺时针方向旋转后恰好与△DAE重合,若AE=3,BF=2,则四边形BFDE的面积是25. 分析 由旋转得到△CDF≌△ADE即S△CDF=S△ADE,求正方形ABCD的面积即可.
解答 解:由旋转得,CD=AD,DF=DE,CF=AE,
在△CDF和△ADE中,
$\left\{\begin{array}{l}{CD=AD}\\{DF=DE}\\{CF=AE}\end{array}\right.$,
∴△CDF≌△ADE,
∴CF=AE=3,S△CDF=S△ADE,
∴S四边形BFDE=S正方形ABCD=(CF+BF)2=(3+2)2=25.
故答案为25.
点评 此题是旋转的性质题,主要考查了正方形的性质,三角形的全等的性质和判定,解本题的关键是面积的转化,S△CDF=S△ADE.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
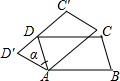 如图,在平行四边形ABCD中,∠BAD=110°,将四边形BCD绕点A逆时针旋转到平行四边形AB′C′D′的位置,旋转角α(0°<α<70°),若C′D′恰好经过点D,则α的度数为40°.
如图,在平行四边形ABCD中,∠BAD=110°,将四边形BCD绕点A逆时针旋转到平行四边形AB′C′D′的位置,旋转角α(0°<α<70°),若C′D′恰好经过点D,则α的度数为40°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在一次课外实践活动中,同学们要测量某公园人工湖两侧A,B两个凉亭之间的距离.现测得AC=50m,BC=100m,∠CAB=120°,请计算A,B两个凉亭之间的距离.
在一次课外实践活动中,同学们要测量某公园人工湖两侧A,B两个凉亭之间的距离.现测得AC=50m,BC=100m,∠CAB=120°,请计算A,B两个凉亭之间的距离.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com