
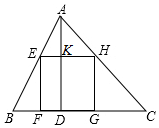
 若正方形有两个相邻顶点在三角形的同一条边上,其余两个顶点分别在三角形的另两条边上,则正方形称为三角形该边上的内接正方形,△ABC中,设BC=a,AC=b,AB=c,各边上的高分别记为ha,hb,hc,各边上的内接正方形的边长分别记为xa,xb,xc
若正方形有两个相邻顶点在三角形的同一条边上,其余两个顶点分别在三角形的另两条边上,则正方形称为三角形该边上的内接正方形,△ABC中,设BC=a,AC=b,AB=c,各边上的高分别记为ha,hb,hc,各边上的内接正方形的边长分别记为xa,xb,xc分析 (1)先根据EH∥FG,判定△AEH∽△ABC,再根据相似三角形对应边成比例,列出比例式变形即可得到$\frac{1}{a}$+$\frac{1}{{h}_{a}}$=$\frac{1}{{x}_{a}}$;
(2)先根据(1)中的结论得出$\frac{1}{b}+\frac{1}{{h}_{b}}=\frac{1}{{x}_{b}}$,再将hb=c和xb=2代入变形,即可求得$\frac{1}{b}$+$\frac{1}{c}$的值;
(3)先根据(1)中的结论得出$\frac{1}{b}+\frac{1}{{h}_{b}}=\frac{1}{{x}_{b}}$和$\frac{1}{c}+\frac{1}{{h}_{c}}=\frac{1}{{x}_{c}}$,变形得出${x}_{b}=\frac{b{h}_{b}}{b+{h}_{b}}$,${x}_{c}=\frac{c{h}_{c}}{c+{h}_{c}}$,再根据△ABC得到bhb=chc,hb=csinA,hc=bsinA,最后代入代数式$\frac{1}{{x}_{b}}-\frac{1}{{x}_{c}}$进行变形推导,即可得出xb与xc的大小关系.
解答  解:∵正方形EFGH中,EH∥FG,
解:∵正方形EFGH中,EH∥FG,
∴△AEH∽△ABC,
∵AD⊥BC,
∴$\frac{EH}{BC}$=$\frac{AK}{AD}$,即$\frac{{x}_{a}}{a}=\frac{{h}_{a}-{x}_{a}}{{h}_{a}}$,
∴$\frac{1}{a}$+$\frac{1}{{h}_{a}}$=$\frac{1}{{x}_{a}}$;
(2)由(1)得:$\frac{1}{b}+\frac{1}{{h}_{b}}=\frac{1}{{x}_{b}}$,
∵∠A=90°,
∴hb=c,
又∵xb=2,
∴$\frac{1}{b}+\frac{1}{c}=\frac{1}{2}$;
(3)xb>xc.
证明:由(1)得:$\frac{1}{b}+\frac{1}{{h}_{b}}=\frac{1}{{x}_{b}}$,$\frac{1}{c}+\frac{1}{{h}_{c}}=\frac{1}{{x}_{c}}$,
∴${x}_{b}=\frac{b{h}_{b}}{b+{h}_{b}}$,${x}_{c}=\frac{c{h}_{c}}{c+{h}_{c}}$,
∵S=$\frac{1}{2}$bhb=$\frac{1}{2}$chc,
∴2S=bhb=chc,
又∵hb=csinA,hc=bsinA,
∴$\frac{1}{{x}_{b}}-\frac{1}{{x}_{c}}$=$\frac{b+{h}_{b}-(c+{h}_{c})}{2S}$
=$\frac{b+csinA-(c+bsinA)}{2S}$
=$\frac{(b-c)(1-sibA)}{2S}$,
∵b<c,sinA<1,
∴$\frac{(b-c)(1-sibA)}{2S}$<0,即$\frac{1}{{x}_{b}}-\frac{1}{{x}_{c}}$<0,
∴xb>xc.
点评 本题主要考查了三角形的综合运用,难度较大,解决问题的关键是掌握相似三角形的判定与性质.解题时注意,当三角形的高出现时,可以考虑相似三角形的对应高之比等于相似比;其中第(2)个问题也可以运用相似三角形的性质进行计算求解.此外,特殊应用和拓展延伸部分的解答都运用了模拟探究中的结论.


科目:初中数学 来源: 题型:选择题
| A. | -4 | B. | -2 | C. | 2 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,小明想通过测量知道一建筑物AB的高度.他通过测量获得了以下的数据:站在点C处测得建筑物顶端A的仰角为48°,他的眼睛距离地面的高度CD=1.6m,C,B间的距离为12m.请你根据测量获得的数据,计算出建筑物AB的高度是多少?
如图,小明想通过测量知道一建筑物AB的高度.他通过测量获得了以下的数据:站在点C处测得建筑物顶端A的仰角为48°,他的眼睛距离地面的高度CD=1.6m,C,B间的距离为12m.请你根据测量获得的数据,计算出建筑物AB的高度是多少?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
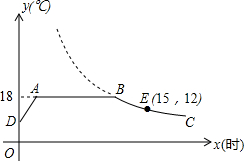 我市某花卉生产基地在气温较低时,用装有恒温系统的温室栽培一种在自然光照且温度为18℃的条件下生长最快的新品种,如图是某天恒温系统从开启到关闭及关闭后,温室内温度y(℃)随时间x(小时)变化的函数图象,其中DA段所满足的表达式为y=5x+13,BC段是反比例函数图象的一部分,点E是BC段上一点.请根据图中信息解答下列问题:
我市某花卉生产基地在气温较低时,用装有恒温系统的温室栽培一种在自然光照且温度为18℃的条件下生长最快的新品种,如图是某天恒温系统从开启到关闭及关闭后,温室内温度y(℃)随时间x(小时)变化的函数图象,其中DA段所满足的表达式为y=5x+13,BC段是反比例函数图象的一部分,点E是BC段上一点.请根据图中信息解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com