
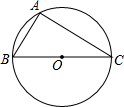
 如图,已知BC为⊙O的直径,△ABC内接于⊙O,AB=2,∠C=30°.
如图,已知BC为⊙O的直径,△ABC内接于⊙O,AB=2,∠C=30°.分析 (1)作BC的垂直平分线交⊙O于点D,连结AD,则AD平分∠BAC;
(2)连结OA,如图,根据圆周角定理得到∠BAC=90°,则∠B=60°,于是可判断△OAB为等边三角形,所以OB=AB=2,∠AOB=60°,再计算出∠AOD,然后根据弧长公式计算$\widehat{AD}$的长.
解答 解:(1)如图,AD为所作;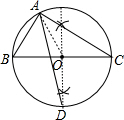
(2)连结OA,如图,
∵BC为⊙O的直径,
∴∠BAC=90°,
在Rt△ABC中,∵∠C=30°,
∴∠B=60°,
而OA=OB,
∴△OAB为等边三角形,
∴OB=AB=2,∠AOB=60°,
而OD⊥BC,
∴∠AOD=60°+90°=150°,
∴$\widehat{AD}$的长度=$\frac{150•π•2}{180}$=$\frac{5}{3}$π.
点评 本题考查了作图-复杂作图:复杂作图是在五种基本作图的基础上进行作图,一般是结合了几何图形的性质和基本作图方法.解决此类题目的关键是熟悉基本几何图形的性质,结合几何图形的基本性质把复杂作图拆解成基本作图,逐步操作.也考查了弧长公式.


科目:初中数学 来源: 题型:填空题
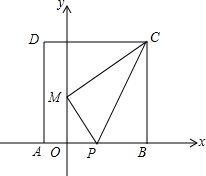 将正方形ABCD放置在如图所示的直角坐标系中,点B的坐标为(8,0),点P在边AB的中点.连结CP,将△BCP沿PC折叠,使点B落在y轴的M点处,且点M的纵坐标为4.若点Q是x轴正半轴上一个运动的点,连结MQ、CQ,则△CMQ周长的最小值为10+2$\sqrt{65}$.
将正方形ABCD放置在如图所示的直角坐标系中,点B的坐标为(8,0),点P在边AB的中点.连结CP,将△BCP沿PC折叠,使点B落在y轴的M点处,且点M的纵坐标为4.若点Q是x轴正半轴上一个运动的点,连结MQ、CQ,则△CMQ周长的最小值为10+2$\sqrt{65}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
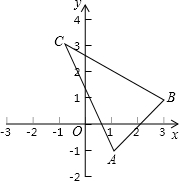 如图,△ABC在平面直角坐标系中,点A(1,-1),点B(3,1),点C(-1,3),将△ABC绕点O旋转90°后得△A1,B1,C1,求点A1,B1,C1的坐标.
如图,△ABC在平面直角坐标系中,点A(1,-1),点B(3,1),点C(-1,3),将△ABC绕点O旋转90°后得△A1,B1,C1,求点A1,B1,C1的坐标.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1:2 | B. | 2:1 | C. | 2:3 | D. | 3:2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com