
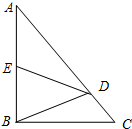
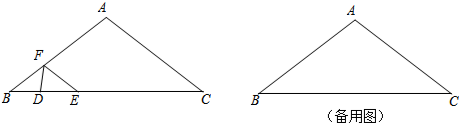
 如图,在Rt△ABC中,∠ABC=90°,点D在边AC上,线段DB绕点D顺时针旋转,端点B恰巧落在边AB上的点E处.如果$\frac{AE}{EB}$=y,$\frac{AD}{DC}$=x.那么y与x满足的关系式是:y=$\frac{x-1}{2}$(用含x的代数式表示y).
如图,在Rt△ABC中,∠ABC=90°,点D在边AC上,线段DB绕点D顺时针旋转,端点B恰巧落在边AB上的点E处.如果$\frac{AE}{EB}$=y,$\frac{AD}{DC}$=x.那么y与x满足的关系式是:y=$\frac{x-1}{2}$(用含x的代数式表示y). 分析 作DF⊥AB于F,证明DF∥BC,根据平行线分线段成比例定理得到$\frac{AF}{FB}$=$\frac{AD}{DC}$,根据旋转的性质得到EF=FB,整理得到答案.
解答 解: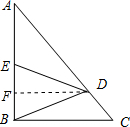 作DF⊥AB于F,又∠ABC=90°,
作DF⊥AB于F,又∠ABC=90°,
∴DF∥BC,
∴$\frac{AF}{FB}$=$\frac{AD}{DC}$=x,
∵DE=DB,DF⊥AB,
∴EF=FB,
∴$\frac{AE}{EB}$=$\frac{x-1}{2}$,
∴y=$\frac{x-1}{2}$,
故答案为:$\frac{x-1}{2}$.
点评 本题考查的是旋转的性质,正确作出辅助线是解题的关键,注意平行线分线段成比例定理和等腰三角形的性质的运用.


 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ①② | B. | ②③ | C. | ②④ | D. | ④⑤ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
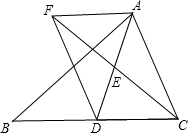 已知:如图,在△ABC中,D是BC边上的一点,连接AD,取AD的中点E,过点A作BC的平行线与CE的延长线交于点F,连接DF.
已知:如图,在△ABC中,D是BC边上的一点,连接AD,取AD的中点E,过点A作BC的平行线与CE的延长线交于点F,连接DF.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
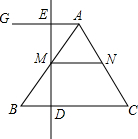 如图,△ABC中,点M是AB边的中点,点D是BC边上一个动点,直线DM交射线AG于点E,AG∥BC.
如图,△ABC中,点M是AB边的中点,点D是BC边上一个动点,直线DM交射线AG于点E,AG∥BC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在平面直角坐标系中,有若干个横坐标分别为整数的点,其顺序按图中“→“方向排列,如(1,0),(2,0),(2,1),(1,1),(1,2),(2,2)…根据这个规律,第82个点的坐标(10,0).
如图,在平面直角坐标系中,有若干个横坐标分别为整数的点,其顺序按图中“→“方向排列,如(1,0),(2,0),(2,1),(1,1),(1,2),(2,2)…根据这个规律,第82个点的坐标(10,0).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com