解:(1)CD=CE;(2分)
(2)∵△ABC是等边三角形
∴AB=AC=BC∠ABC=∠ACB=60°,(4分)
∵BD⊥AC
∴
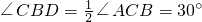
,

,(5分)
∵

∴CD=CE,(6分)
∴∠E=∠CDE,(7分)
∵∠ACB=∠E+∠CDE
∴
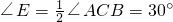
,(8分)
∴∠CBD=∠E,
∴BD=ED,
∴△BDE是等腰三角形.(9分)
分析:(1)CD=CE,理由为:由等边三角形ABC得到∠ABC为60°,又DB垂直AC,根据“三线合一”得到∠DBC为30°,根据直角三角形中,30°角所对的直角边等于斜边的一半得到CD等于BC的一半,由题中已知的CE等于BC的一半,等量代换可得CD=CE;
(2)由等边三角形ABC得到∠ACB为60°,又(1)得到CD=CE,根据“等边对等角”以及外角性质得到∠E=30°,又∠DBC为30°,故两角相等,再根据“等角对等边”得到BD=DE,即三角形BDE为等腰三角形.
点评:此题考查了等边三角形的性质,直角三角形的性质以及等腰三角形的判定.利用等腰三角形的性质可以解决证明角、边的相等问题,尤其在证明其性质和判定中展示的转换意识,对同学们分析和解决问题能力的提高有非常重要的价值.

 如图,BD是等边△ABC的高,E是BC延长线上一点,且
如图,BD是等边△ABC的高,E是BC延长线上一点,且 .
.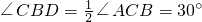 ,
, ,(5分)
,(5分)
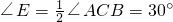 ,(8分)
,(8分)

 如图,BD是等边△ABC一边上的高,延长BC至E,使CE=CD,
如图,BD是等边△ABC一边上的高,延长BC至E,使CE=CD,