
【题目】如图,在△ABC中,AB=AC,以AB为直径的⊙O交BC边于点D,交AC边于点E.过点D作⊙O的切线,交AC于点F,交AB的延长线于点G,连接DE. 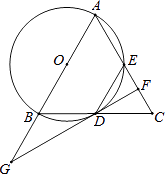
(1)求证:BD=CD;
(2)若∠G=40°,求∠AED的度数.
(3)若BG=6,CF=2,求⊙O的半径.
【答案】
(1)证明:连接AD,
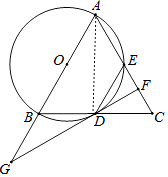
∵AB为直径,
∴∠ACB=90°,
∴AD⊥BC,
∵AB=AC,
∴BD=CD
(2)解:连接OD,
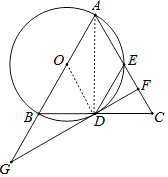
∵GF是切线,OD是半径,
∴OD⊥GF,
∴∠ODG=90°,
∵∠G=40°,
∴∠GOD=50°,
∵OB=OD,
∴∠OBD=65°,
∵点A、B、D、E都在⊙O上,
∴∠ABD+∠AED=180°,
∴∠AED=115°
(3)解:∵AB=AC,
∴∠ABC=∠C,
∵OB=OD,
∴∠ABC=∠ODB,
∴∠ODB=∠C,
∴OD∥AC,
∴△GOD∽△GAF,
∴ ![]() =
= ![]() ,
,
∴设⊙O的半径是r,则AB=AC=2r,
∴AF=2r﹣2,
∴ ![]() =
= ![]() ,
,
∴r=3,
即⊙O的半径是3
【解析】(1)连接AD,根据圆周角定理得出AD⊥BC,根据等腰三角形的性质得出即可;(2)连接OD,根据切线的性质求出∠ODG=90°,求出∠BOD、∠ABC,根据圆内接四边形求出即可;(3)求出△ODG∽△AFG,得出比例式,即可求出圆的半径.
【考点精析】根据题目的已知条件,利用等腰三角形的性质和切线的性质定理的相关知识可以得到问题的答案,需要掌握等腰三角形的两个底角相等(简称:等边对等角);切线的性质:1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径.


科目:初中数学 来源: 题型:
【题目】九年级(1)班和(2)班分别有一男一女共4名学生报名参加学校文艺汇演主持人的选拔.
(1)若从报名的4名学生中随机选1名,则所选的这名学生是女生的概率是 .
(2)若从报名的4名学生中随机选2名,用树状图或表格列出所有可能的情况,并求出这2名学生来自同一个班级的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
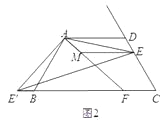
【题目】已知:四边形ABCD中,AD∥BC,AD=AB=CD,∠BAD=120°,点E是射线CD上的一个动点(与C、D不重合),将△ADE绕点A顺时针旋转120°后,得到△ABE',连接EE'.
(1)如图1,∠AEE'= °;
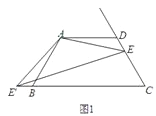
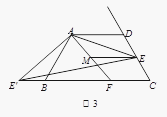
(2)如图2,如果将直线AE绕点A顺时针旋转30°后交直线BC于点F,过点E作EM∥AD交直线AF于点M,写出线段DE、BF、ME之间的数量关系;
(3)如图3,在(2)的条件下,如果CE=2,AE=![]() ,求ME的长.
,求ME的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一次“探究性学习”课中,李老师设计了如下数表:
n | 2 | 3 | 4 | 5 | … |
a | 22﹣1 | 32﹣1 | 42﹣1 | 52﹣1 | … |
b | 4 | 6 | 8 | 10 | … |
c | 22+1 | 32+1 | 42+1 | 52+1 | … |
(1)用含自然数n(n>1)的代数式表示:a,b,c.
(2)当c=101时,求n的值;
(3)用等式表示a、b、c之间的数量关系
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若10m=5,10n=3,则102m+3n= .
【答案】675.
【解析】102m+3n=102m103n=(10m)2(10n)3=5233=675,
故答案为:675.
点睛:此题考查了幂的乘方与积的乘方, 同底数幂的乘法. 首先根据同底数幂的乘法法则,可得102m+3n=102m×103n,然后根据幂的乘方的运算方法,可得102m×103n=(10m)2×(10n)3,最后把10m=5,10n=2代入化简后的算式,求出102m+3n的值是多少即可.
【题型】填空题
【结束】
18
【题目】计算:
(1)(5mn2﹣4m2n)(﹣2mn)
(2)(x+7)(x﹣6)﹣(x﹣2)(x+1)
(3) (-![]() )2 016×161 008;
)2 016×161 008;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,直线y= ![]() x经过点A,作AB⊥x轴于点B,将△ABO绕点B逆时针旋转60°得到△CBD,若点B的坐标为(2,0),则点C的坐标为 .
x经过点A,作AB⊥x轴于点B,将△ABO绕点B逆时针旋转60°得到△CBD,若点B的坐标为(2,0),则点C的坐标为 . 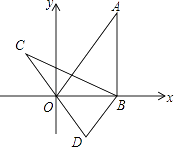
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠MON=30°,点A1,A2,A3,…在射线ON上,点B1,B2,B3,…在射线OM上,△A1B1A2,△A2B2A3,△A3B3A4,…均为等边三角形,若OA2=4,则△AnBnAn+1的边长为__________.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com