
【题目】已知:AD是△ABC的高,且BD=CD.
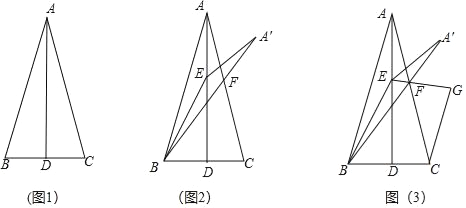
(1)如图1,求证:∠BAD=∠CAD;
(2)如图2,点E在AD上,连接BE,将△ABE沿BE折叠得到△A′BE,A′B与AC相交于点F,若BE=BC,求∠BFC的大小;
(3)如图3,在(2)的条件下,连接EF,过点C作CG⊥EF,交EF的延长线于点G,若BF=10,EG=6,求线段CF的长.
【答案】(1)证明见解析;(2)∠BFC=60°;(3)CF=8.
【解析】
(1)易得AB=AC,∠BAD=∠CAD.
(2) 连接EC, 可证得△BCE是等边三角形,∠BEC=60°,∠BED=30°且由翻折的性质可知:∠ABE=∠A′BE=![]() ∠ABF,可得∠BFC=∠FAB+∠FBA=2(∠BAE+∠ABE)=2∠BED=60°.
∠ABF,可得∠BFC=∠FAB+∠FBA=2(∠BAE+∠ABE)=2∠BED=60°.
(3) 连接EC,作EH⊥AB于H,EN⊥AC于N,EM⊥BA′于M, 可证得Rt△EMB≌Rt△ENC,
BM=CN,BF﹣FM=CF+FN,可得CF的值.
(1)证明:如图1中,
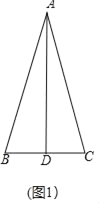
∵BD=CD,AD⊥BC,
∴AB=AC,
∴∠BAD=∠CAD.
(2)解:如图2中,连接EC.
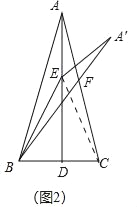
∵BD⊥BC,BD=CD,
∴EB=EC,
又∵EB=BC,
∴BE=EC=BC,
∴△BCE是等边三角形,
∴∠BEC=60°,
∴∠BED=30°,
由翻折的性质可知:∠ABE=∠A′BE=![]() ∠ABF,
∠ABF,
∴∠ABF=2∠ABE,由(1)可知∠FAB=2∠BAE,
∴∠BFC=∠FAB+∠FBA=2(∠BAE+∠ABE)=2∠BED=60°.
(3)解:如图3中,连接EC,作EH⊥AB于H,EN⊥AC于N,EM⊥BA′于M.

∵∠BAD=∠CAD,∠ABE=∠A′BE,
∴EH=EN=EM,
∴∠AFE=∠EFB,
∵∠BFC=60°,
∴∠AFE=∠BFE=60°,
在Rt△EFM中,∵∠FEM=90°﹣60°=30°,
∴EF=2FM,设FM=m,则EF=2m,
∴FG=EG﹣EF=6﹣2m,
易知:FN=![]() EF=m,CF=2FG=12﹣4m,
EF=m,CF=2FG=12﹣4m,
∵∠EMB=∠ENC=90°,EB=EC,EM=EN,
∴Rt△EMB≌Rt△ENC(HL),
∴BM=CN,
∴BF﹣FM=CF+FN,
∴10﹣m=12﹣4m+m,
∴m=1,
∴CF=12﹣4=8.


 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:初中数学 来源: 题型:
【题目】同时抛掷两枚材质均匀的正方体骰子,
(1)通过画树状图或列表,列举出所有向上点数之和的等可能结果;
(2)求向上点数之和为8的概率![]() ;
;
(3)求向上点数之和不超过5的概率![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中抛物线y=(x+1)(x﹣3)与x轴相交于A、B两点,若在抛物线上有且只有三个不同的点C1、C2、C3,使得△ABC1、△ABC2、△ABC3的面积都等于m,则m的值是( )
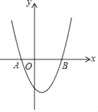
A. 6 B. 8 C. 12 D. 16
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将矩形ABCO放在直角坐标系中,其中顶点B的坐标为(10, 8),E是BC边上一点将△ABE沿AE折叠,点B刚好与OC边上点D重合,过点E的反比例函数y=![]() 的图象与边AB交于点F, 则线段AF的长为( )
的图象与边AB交于点F, 则线段AF的长为( )

A. ![]() B. 2 C.
B. 2 C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
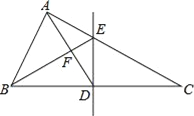
【题目】如图,在△ABC中,BC的垂直平分线分别交BC,AC于点D,E,BE交AD于点F,AB=AD.
(1)判断△FDB与△ABC是否相似,并说明理由.
(2)AF与DF相等吗?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“十九大”报告提出了我国将加大治理环境污染的力度,还我青山绿水,其中雾霾天气让环保和健康问题成为焦点,为了调查学生对雾霾天气知识的了解程度,某校在全校学生中抽取400名同学做了一次调查,根据调查统计结果,绘制了不完整的一种统计图表.
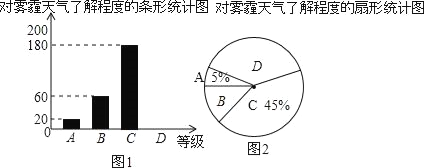
对雾霾了解程度的统计表
对雾霾的了解程度 | 百分比 |
A.非常了解 | 5% |
B.比较了解 | m |
C.基本了解 | 45% |
D.不了解 | n |
请结合统计图表,回答下列问题:
(1)统计表中:m= ,n= ;
(2)请在图1中补全条形统计图;
(3)请问在图2所示的扇形统计图中,D部分扇形所对应的圆心角是多少度?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】去学校食堂就餐,经常会在一个买菜窗口前等待,经调查发现,同学的舒适度指数y与等时间x(分)之间满足反比例函数关系,如下表:
等待时间x | 1 | 2 | 5 | 10 | 20 |
舒适度指数y | 100 | 50 | 20 | 10 | 5 |
已知学生等待时间不超过30分钟
(1)求y与x的函数关系式,并写出自变量x的取值范围.
(2)若等待时间8分钟时,求舒适度的值;
(3)舒适度指数不低于10时,同学才会感到舒适.请说明,作为食堂的管理员,让每个在窗口买菜的同学最多等待多少时间?
查看答案和解析>>
科目:初中数学 来源: 题型:
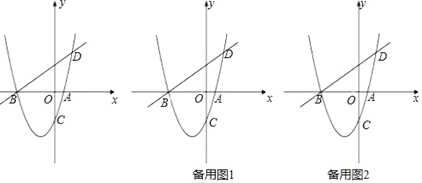
【题目】(12分)如图,已知抛物线y=ax2+bx﹣2(a≠0)与x轴交于A、B两点,与y轴交于C点,直线BD交抛物线于点D,并且D(2,3),B(﹣4,0).
(1)求抛物线的解析式;
(2)已知点M为抛物线上一动点,且在第三象限,顺次连接点B、M、C,求△BMC面积的最大值;
(3)在(2)中△BMC面积最大的条件下,过点M作直线平行于y轴,在这条直线上是否存在一个以Q点为圆心,OQ为半径且与直线AC相切的圆?若存在,求出圆心Q的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com