
分析 (1)①根据配方法可以说明多项式x2-4x+5的值一定大于零;
②根据配方法和①中的结论可以求得分式$\frac{5{x}^{2}-20x+27}{{x}^{2}-4x+5}$的最大值;
(2)根据题意可以求得M-N的差,然后分段进行讨论,即可解答本题.
解答 解:(1)①∵x2-4x+5=(x-2)2+1≥1>0,
∴多项式x2-4x+5的值一定大于零;
②$\frac{5{x}^{2}-20x+27}{{x}^{2}-4x+5}$=$\frac{5({x}^{2}-4x+5)+2}{{x}^{2}-4x+5}$=5+$\frac{2}{{x}^{2}-4x+5}$,
由①知,当x=2时,x2-4x+5取得最小值1,
∴5+$\frac{2}{{x}^{2}-4x+5}$≤5+$\frac{2}{1}$=7,
∴分式$\frac{5{x}^{2}-20x+27}{{x}^{2}-4x+5}$的最大值是7;
(2)∵x>2,M=5x2+3,N=4x(x+1),
∴M-N=(5x2+3)-4x(x+1)=5x2+3-4x2-4x=x2-4x+3=(x-1)(x-3),
∴当2<x<3时,M-N=(x-1)(x-3)<0,则M<N,
当x=3时,M-N=(x-1)(x-3)=0,则M=N,
当x>3时,M-N=(x-1)(x-3)>0,则M>N.
点评 本题考查配方法的应用、非负数的性质、完全平方式,解答本题的关键是明确题意,找出所求问题需要的条件,利用配方法解答问题.


科目:初中数学 来源: 题型:解答题
| 级数 | 全月应纳税所得额 | 税率% |
| 1 | 不超过500元的部分 | 5 |
| 2 | 超过500元至2000元的部分 | 10 |
| 3 | 超过2000元至5000元的部分 | 15 |
| 4 | 超过5000元至20000元的部分 | 20 |
| … | … |
| 公民 | 工资薪金(元) | 应纳税金(元) |
| 甲 | 2000 | 0 |
| 乙 | 2500 | 25 |
| 丙 | 3900 | 165 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{x+1}+\sqrt{x+2}+3=0$ | B. | $\sqrt{x-9}+\sqrt{4-x}=16$ | ||
| C. | $\sqrt{{x}^{2}+1}-\sqrt{{x}^{2}+2}=1-\frac{1}{\sqrt{{x}^{2}+1}}$ | D. | 6$\sqrt{{x}^{2}-2x+6}=21+2x-{x}^{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 蔗糖质量 | 4.5 | 5.8 | 5.4 | 6.9 | 4.2 | 7 | 4.9 | 5.8 | 9.8 | 6.8 |
| 编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 蔗糖质量 | 7.4 | 4.9 | 7.8 | 4.1 | 7.2 | 5.8 | 7.6 | 6.8 | 4.5 | 4.9 |
| 酸奶口感最佳的杯数(杯) | 每杯酸奶中添加的蔗糖克数平均值(克) | 每杯酸奶中添加的蔗糖克数的方差 | |
| 学农1班 | x | 6.11 | 2.39 |
| 学农2班 | 6 | 6.1 | 1.81 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
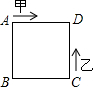 如图,甲、乙两动点分别从正方形ABCD的顶点A、C同时沿正方形的边开始移动,甲点依顺时针方向环行,乙点依逆时针方向环行,若乙的速度是甲的速度的4倍,则它们第16次相遇在边( )
如图,甲、乙两动点分别从正方形ABCD的顶点A、C同时沿正方形的边开始移动,甲点依顺时针方向环行,乙点依逆时针方向环行,若乙的速度是甲的速度的4倍,则它们第16次相遇在边( )| A. | AB上 | B. | BC上 | C. | CD上 | D. | DA上 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com