
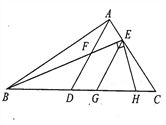
【题目】如图,在△ABC中,点D在BC 上,点E 在AC 上,AD交BE于F. 已知EG∥AD交BC于G, EH⊥BE交BC于H,∠HEG = 50°.
(1)求∠BFD的度数.
(2)若∠BAD = ∠EBC,∠C = 41°,求∠BAC的度数.
【答案】(1)∠BFD=40°(2)∠BAC=99°
【解析】(1)根据垂直的定义可得∠BEH=90°,然后求出∠BEG=40°,再根据两直线平行线,同位角相等可得∠BFD=∠BEG;
(2)根据三角形的一个外角等于与它不相邻的两个内角的和可得∠BFD=∠EBC+∠ABE=∠ABC,然后根据三角形的内角和定理列式计算即可得解.
试题解析:(1)∵EH⊥BE,
∴∠BEH=90°,
∵∠HEG=50°,
∴∠BEG=40°,
又∵EG∥AD,
∴∠BFD=∠BEG=40°;
(2)∵∠BFD=∠BAD+∠ABE,∠BAD=∠EBC,
∴∠BFD=∠EBC+∠ABE=∠ABC=40°,
∵∠C=41°,
∴∠BAC=180°-∠ABC-∠C=180°-40°-41°=99°.


 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,边长为6的正六边形ABCDEF的对称中心与原点O重合,点A在x轴上,点B在反比例函数 ![]() 位于第一象限的图象上,则k的值为( )
位于第一象限的图象上,则k的值为( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在y轴右侧且平行于y轴的直线l被反比例函数![]() (
(![]() )与函数
)与函数![]() (
(![]() )所截,当直线l向右平移4个单位时,直线l被两函数图象所截得的线段扫过的面积为__________平方单位.
)所截,当直线l向右平移4个单位时,直线l被两函数图象所截得的线段扫过的面积为__________平方单位.

【答案】8
【解析】∵y轴右侧且平行于y轴的直线l被反比例函数y=![]() (x>0)与函数y=
(x>0)与函数y=![]() +2(x>0)所截,∴设它们的交点为A,C,∴AC=2,∵直线l向右平移4个单位,∴CD=4,∴直线l被两函数图象所截得的线段扫过的面积为 2×4=8平方单位.故答案为8.
+2(x>0)所截,∴设它们的交点为A,C,∴AC=2,∵直线l向右平移4个单位,∴CD=4,∴直线l被两函数图象所截得的线段扫过的面积为 2×4=8平方单位.故答案为8.

【题型】填空题
【结束】
14
【题目】函数![]() 的图象如右图所示,则结论:
的图象如右图所示,则结论:
①两函数图象的交点![]() 的坐标为
的坐标为![]() ; ②当
; ②当![]() 时,
时, ![]() ;
;
③当![]() 时,
时, ![]() ; ④当
; ④当![]() 逐渐增大时,
逐渐增大时, ![]() 随着
随着![]() 的增大而增大,
的增大而增大, ![]() 随着
随着![]() 的增大而减小.
的增大而减小.
其中正确结论的序号是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有下列说法:①若DE∥AB,则∠DEF+∠EFB=180;
②能与∠DEF构成内错角的角的个数有2个;③能与∠BFE构
成同位角的角的个数有2个;④能与∠C构成同旁内角的角的个数有4个.其中结论正确的是( )
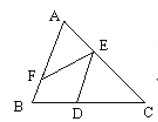
A. ①② B. ③④ C. ①③④ D. ①②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图17-Z-12所示,等腰三角形ABC的底边长为8 cm,腰长为5 cm,一动点P在底边上从点B向点C以0.25 cm/s的速度移动,请你探究:当点P运动几秒时,点P与顶点A的连线AP与腰垂直?

图17-Z-12
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角梯形ABCD中,AD∥BC,∠C=90°,AD=5,BC=9,以A为中心将腰AB顺时针旋转90°至AE,连接DE,则△ADE的面积等于( )
A.10
B.11
C.12
D.13
查看答案和解析>>
科目:初中数学 来源: 题型:
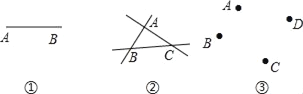
【题目】观察图①,由点A和点B可确定 条直线;
观察图②,由不在同一直线上的三点A、B和C最多能确定 条直线;
(1)动手画一画图③中经过A、B、C、D四点的所有直线,最多共可作 条直线;
(2)在同一平面内任三点不在同一直线的五个点最多能确定 条直线、n个点(n≥2)最多能确定 条直线.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,线段AB和射线BM交于点B.
(1)利用尺规完成以下作图,并保留作图痕迹(不写作法)
①在射线BM上作一点C,使AC=AB;
②作∠ABM 的角平分线交AC于D点;
③在射线CM上作一点E,使CE=CD,连接DE.

(2)在(1)所作的图形中,猜想线段BD与DE的数量关系,并证明之.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com