Question

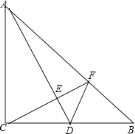
【题目】如图,在Rt△ABC中,∠ACB=90,AC=BC，点D为BC的中点，CE⊥AD于点E，其延长线交AB于点F，连接DF.求证：∠ADC=∠BDF.

Answer 1

【答案】证明见解析.

【解析】

作BG⊥CB，交CF的延长线于点G，由ASA证明△ACD≌△CBG，得出CD=BG，∠CDA=∠CGB，证出BG=BD，∠FBD=∠GBF=∠CBG，再由SAS证明△BFG≌△BFD，得出∠FGB=∠FDB，即可得出结论．

证明：作BG⊥CB，交CF的延长线于点G，如图所示：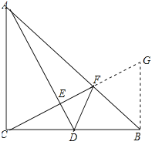

∵∠CBG=90°，CF⊥AD，
∴∠CAD+∠ADC=∠BCG+∠ADC=90°，
∴∠CAD=∠BCG，
在△ACD和△CBG中，
，
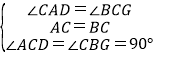∴△ACD≌△CBG（ASA），
∴CD=BG，∠CDA=∠CGB，
∵CD=BD，
∴BG=BD，
∵∠ABC=45°，
∴∠FBD=∠GBF=∠CBG，
在△BFG和△BFD中，

∴△BFG≌△BFD（SAS），
∴∠FGB=∠FDB，
∴∠ADC=∠BDF．