
分析 (1)先化简括号内的式子,再根据分式的乘法可以化简本题;
(2)先将原式展开,然后根据完全平方公式可以对式子分解因式.
解答 解:(1)($\frac{{x}^{2}}{x-2}$-$\frac{4}{x-2}$)•$\frac{1}{{x}^{2}+2x}$
=$\frac{{x}^{2}-4}{x-2}•\frac{1}{x(x+2)}$
=$\frac{(x+2)(x-2)}{x-2}•\frac{1}{x(x+2)}$
=$\frac{1}{x}$;
(2)(x-1)(x-3)+1
=x2-4x+3+1
=x2-4x+4
=(x-2)2.
点评 本题考查分式的混合运算、因式分解-运用公式法,解题的关键是明确分式的混合运算的计算方法、会用公式法分解因式.


科目:初中数学 来源: 题型:选择题
| A. | 96人 | B. | 90人 | C. | 64人 | D. | 50人 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
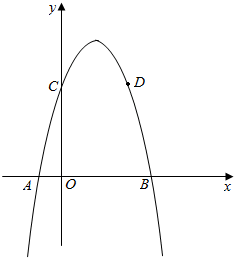 已知:抛物线y=-x2+bx+c的图象交y轴于C,交x轴交于A、B两点,抛物线经过点D(4,5),C、D两点关于抛物线的对称轴对称.
已知:抛物线y=-x2+bx+c的图象交y轴于C,交x轴交于A、B两点,抛物线经过点D(4,5),C、D两点关于抛物线的对称轴对称.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 菱形ABCD中,∠B=60°,延长BC至E,使得CE=BC,点F在DE上,DF=6,AG平分∠BAF,与线段BC相交于点G,若CG=2,则线段AB的长度为10.
菱形ABCD中,∠B=60°,延长BC至E,使得CE=BC,点F在DE上,DF=6,AG平分∠BAF,与线段BC相交于点G,若CG=2,则线段AB的长度为10.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | m≥6 | B. | m≥8 | C. | m≥9 | D. | m≥12 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x≥6 | B. | x≥0 | C. | 0≤x≤6 | D. | x为一切实数 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com