
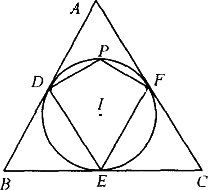
如图,已知△ABC的内切圆⊙I切三边于D、E、F,若∠BAC=70°,P为![]() 上任意一点.试求∠DEF和∠DPF的度数.
上任意一点.试求∠DEF和∠DPF的度数.
|
解:连结ID、IF, ∵⊙I为△ABC的内切圆,切点为D、E、F, ∴ID⊥AB,IF⊥AC, ∴∠A+∠DIF=180°, 又∵∠BAC=70°, ∴∠DIF=110°,∠DEF= 又四边形DEFP内接于⊙I, ∴∠DPF=180°-∠DEF=125°.
思路点拨:因为∠DEF是圆周角,所以可先求相应的圆心角∠DIF,根据内心的性质.知ID⊥AB,IF⊥AC,从而可找出∠A与∠DIF的关系,可求出∠DIF,再根据圆的内接四边形的性质求出∠DPF. 评注:①本题是有关内切圆的又一典型问题,常作出内心到三边的距离,构造直角三角形解题. ②一般地,已知∠A与∠DEF中之一,可求出另一角,它们的关系式为:∠DEF=90°- |


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
| AA1 |
| AB |
| BB1 |
| BC |
| CC1 |
| CA |
| 1 |
| 2 |
| 1 |
| 4 |
| AA2 |
| AB |
| BB2 |
| BC |
| CC2 |
| CA |
| 1 |
| 3 |
| 1 |
| 3 |
| AA3 |
| AB |
| BB3 |
| BC |
| CC3 |
| CA |
| 1 |
| 4 |
| 7 |
| 16 |
| AA8 |
| AB |
| BB8 |
| BC |
| CC8 |
| CA |
| 1 |
| 9 |

查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,已知△ABC的面积为4,且AB=AC,现将△ABC沿CA方向平移CA的长度,得到△EFA.
如图,已知△ABC的面积为4,且AB=AC,现将△ABC沿CA方向平移CA的长度,得到△EFA.查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
 (2010•孝感模拟)如图,已知△ABC的三个顶点的坐标分别为A(-2,2)、B(-5,0)、C(-1,0).
(2010•孝感模拟)如图,已知△ABC的三个顶点的坐标分别为A(-2,2)、B(-5,0)、C(-1,0).查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,已知△ABC的三个顶点的坐标分别是A(-7,1),B(-3,3),C(-2,6).
如图,已知△ABC的三个顶点的坐标分别是A(-7,1),B(-3,3),C(-2,6).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com