
【题目】已知如图,在数轴上有A,B两点,所表示的数分别为-10,4,点A以每秒5个单位长度的速度向右运动,同时点B以每秒3个单位长度的速度也向左运动,如果设运动时间为t秒,解答下列问题:![]()
(1)运动前线段AB的长为 ; 运动1秒后线段AB的长为 ;
(2)运动t秒后,点A,点B运动的距离分别为 ;用t表示A,B分别为 .
(3)求t为何值时,点A与点B恰好重合;
(4)在上述运动的过程中,是否存在某一时刻t,使得线段AB的长为6,若存在,求t的值; 若不存在,请说明理由.
【答案】(1)14;6;(2)5t,3t;5t-10,4-3t;(3)t=![]() ;(4)t=1秒或
;(4)t=1秒或![]() 秒.
秒.
【解析】
(1)根据数轴上两点间的距离等于右边的数减去左边的数求出AB的长,且求出1秒后AB的长即可;
(2)根据路程=时间×速度分别表示出A,B运动的距离,且分别表示出A,B表示的数即可;
(3)根据A,B表示的数相同列出方程,求出方程的解即可得到t的值;
(4)存在,分两种情况分别求出t的值即可.
(1)运动前线段AB的长为4-(-10)=14;运动1秒后线段AB的长为14-8=6;
(2)运动t秒后,点A,点B运动的距离分别为5t,3t;用t表示A,B分别为5t-10,4-3t;
(3)根据题意得:5t-10=4-3t,
解得:t=![]() ;
;
(4)存在,
当A,B没有相遇时,可得14-8t=6,
解得:t=1;
当A,B错开时,可得8t-14=6,
解得:t=![]() ,
,
综上,当t=1秒或![]() 秒时,线段AB的长为6.
秒时,线段AB的长为6.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】“世界那么大,我想去看看”一句话红遍网络,骑自行车旅行越来越受到人们的喜爱.各种品牌的山地车相继投放市场.顺风车行经营的![]() 型车2018年6月份销售总额为
型车2018年6月份销售总额为![]() 万元,今年经过改造升级后
万元,今年经过改造升级后![]() 型车每辆销售价比去年增加
型车每辆销售价比去年增加![]() 元,若今年6月份与去年6月份卖出的
元,若今年6月份与去年6月份卖出的![]() 型车数量相同,则今年6月份
型车数量相同,则今年6月份![]() 型车销售总额将比去年6月份销售总额增加
型车销售总额将比去年6月份销售总额增加![]() .
.
(1)今年6月份![]() 型车每辆售价多少元?(用列方程的方法解答)
型车每辆售价多少元?(用列方程的方法解答)
(2)已知![]() 两种型号车今年的进货及销售价格如下表:
两种型号车今年的进货及销售价格如下表:
|
| |
进货价格(元/辆) |
|
|
销售价格(元/辆) | 今年的销售价格 |
|
该车行计划7月份进这批![]() 型车和
型车和![]() 型车共
型车共![]() 辆,且
辆,且![]() 型车的进货数量不超过
型车的进货数量不超过![]() 型车数量的两倍,应如何进货才能是这批车获利最多?
型车数量的两倍,应如何进货才能是这批车获利最多?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在我市中小学生“我的中国梦”读书活动中,某校对部分学生做了一次主题为“我最喜爱的图书”的调查活动,将图书分为甲、乙、丙、丁四类,学生可根据自己的爱好任选其中一类。学校根据调查情况进行了统计,并绘制了不完整的条形统计图和扇形统计图。
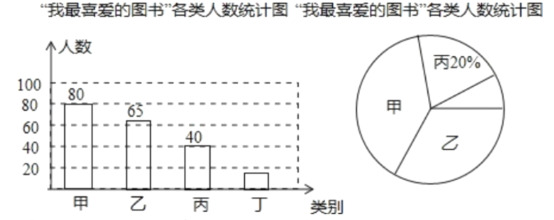
请你结合图中信息,解答下列问题:
(1)本次共调查了___名学生;
(2)被调查的学生中,最喜爱丁类图书的有___人,最喜爱甲类图书的人数占本次被调查人数的___%;
(3)在最喜爱丙类学生的图书的学生中,女生人数是男生人数的1.5倍,若这所学校共有学生1500人,请你估计该校最喜爱丙类图书的女生和男生分别有多少人。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,BD是△ABC的角平分线,点E,F分别在BC、AB上,且DE∥AB,EF∥AC.
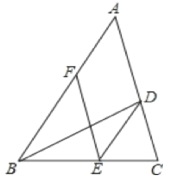
(1)求证:BE=AF;
(2)若∠ABC=60°,BD=6,求四边形ADEF的面积。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)阅读下面材料:
点A、B在数轴上分别表示实数a、b,A、B两点之间的距离表示为|AB|.当A、B两点中有一点在原点时,不妨设点A在原点,如图1,|AB|=|OB|=|b|=|a﹣b|;当A、B两点都不在原点时,
①如图2,点A、B都在原点的右边|AB|=|OB|﹣|OA|=|b|﹣|a|=b﹣a=|a﹣b|;
②如图3,点A、B都在原点的左边,|AB|=|OB|﹣|OA|=|b|﹣|a|=﹣b﹣(﹣a)=|a﹣b|;
③如图4,点A、B在原点的两边,|AB|=|OB|+|OA|=|a|+|b|=a+(﹣b)=|a﹣b|

(2)回答下列问题:
①数轴上表示2和5的两点之间的距离是 ,数轴上表示﹣2和﹣5的两点之间的距离是 ,数轴上表示1和﹣3的两点之间的距离是 ;
②数轴上表示x和﹣1的两点A和B之间的距离是 ,如果|AB|=2,那么x为 ;
③代数式|x+1|+|x﹣2|取最小值时,相应的整数x的取值是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
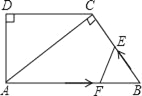
【题目】如图,在直角梯形ABCD中,AB∥DC,∠D=90°,AC⊥BC,AB=10cm,BC=6cm,F点以2cm/秒的速度在线段AB上由A向B匀速运动,E点同时以1cm/秒的速度在线段BC上由B向C匀速运动,设运动时间为t秒(0<t<5).
(1)求证:△ACD∽△BAC;
(2)求DC的长;
(3)设四边形AFEC的面积为y,求y关于t的函数关系式,并求出y的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
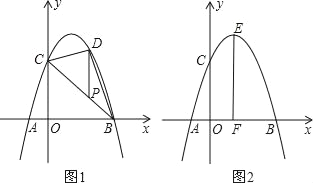
【题目】抛物线y=﹣x2+bx+c经过点A、B、C,已知A(﹣1,0),C(0,3).
(1)求抛物线的解析式;
(2)如图1,P为线段BC上一点,过点P作y轴平行线,交抛物线于点D,当△BDC的面积最大时,求点P的坐标;
(3)如图2,抛物线顶点为E,EF⊥x轴于F点,M(m,0)是x轴上一动点,N是线段EF上一点,若∠MNC=90°,请指出实数m的变化范围,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,点C在⊙O上,∠ABC的平分线与AC相交于点D,与⊙O过点A的切线相交于点E.
(1)∠ACB= °,理由是: ;
(2)猜想△EAD的形状,并证明你的猜想;
(3)若AB=8,AD=6,求BD.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某车间共有75名工人生产A、B两种工件,已知一名工人每天可生产A种工件15件或B种工件20件,但要安装一台机械时,同时需A种工件1件,B种工件2件,才能配套,设车间如何分配工人生产,才能保证连续安装机械时,两种工件恰好配套?
设该车间分配![]() 名工人生产A种工件,
名工人生产A种工件,![]() 名工人生产B种工件才能保证连续安装机械时两种工件恰好配套.
名工人生产B种工件才能保证连续安装机械时两种工件恰好配套. ![]() 的值为( )
的值为( )
A.30B.40C.45D.55
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com