
【题目】如图,矩形ABCD中,AB=16cm,BC=6cm,点P从点A出发沿AB向点B移动(不与点A、B重合),一直到达点B为止;同时,点Q从点C出发沿CD向点D移动(不与点C、D重合).
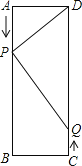
(1)若点P、Q均以3cm/s的速度移动,经过多长时间四边形BPDQ为菱形?
(2)若点P为3cm/s的速度移动,点Q以2cm/s的速度移动,经过多长时间△DPQ为直角三角形?
【答案】见解析
【解析】解:(1)∵四边形ABCD是矩形,
∴AB∥CD.
∵点P、Q均以3cm/s的速度移动,
∴AP=CQ,
∴BP=DQ,
∴四边形BPDQ是平行四边形,
∴当BP=DP时,四边形BPDQ是菱形.
设经过xs,四边形BPDQ是菱形,则有AP=3xcm,BP=(16﹣3x)cm,
由勾股定理得:DP2=(3x)2+62,
∴DP2=(3x)2+62=(16﹣3x)2,
解得:x=![]() .
.
答:经过![]() s时四边形BPDQ是菱形.
s时四边形BPDQ是菱形.
(2)∵点P不与点A重合,
∴∠PDQ≠90°,
∴△DPQ为直角三角形分两种情况:
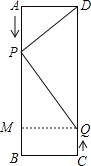
①当∠DPQ=90°时,△DPQ为直角三角形,过点Q作QM⊥AB于M,易得四边形BCQM为矩形,如图所示.
∵AP=3xcm,BM=CQ=2xcm,则PM=(16﹣5x)cm,DQ=(16﹣2x)cm,
∴(16﹣5x)2+62+(3x)2+62=(16﹣2x)2,
解得:x1=2,x2=![]() ;
;
②当∠DQP=90°时,AP+CQ=16,
所以3x+2x=16,解得:x=![]() .
.
综上可知:经过2s、![]() s或
s或![]() s时,△DPQ为直角三角形.
s时,△DPQ为直角三角形.


科目:初中数学 来源: 题型:
【题目】(梅州)下列事件中是必然事件是( )
A、明天太阳从西边升起 B、篮球队员在罚球线投篮一次,未投中
C、实心铁球投入水中会沉入水底 D、抛出一枚硬币,落地后正面向上
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年某县有1万名初中和小学生参加全国义务教育质量抽测,为了了解1万名学生的抽测成绩,从中抽取500名学生抽测成绩进行统计分析,在这个问题中数据500是( )
A. 总体 B. 个体 C. 一个样本 D. 样本容量
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】要证明命题“若a>b,则a2>b2”是假命题,下列a,b的值不能作为反例的是( )
A.a=1,b=﹣2
B.a=0,b=﹣1
C.a=﹣1,b=﹣2
D.a=2,b=﹣1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知x=-1是关于x的方程a+bx=-2的解,则代数式2015-a+b的值为( )
A. 2013 B. 2015 C. 2017 D. 2018
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=5x2向右平移2个单位,再向上平移3个单位,得到的新抛物线的顶点坐标是( )
A.(2,3)
B.(﹣2,3)
C.(2,﹣3)
D.(﹣2,﹣3)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com