
【题目】如图,在Rt△ABC中,AB=BC,∠ABC=90°,点D是AB的中点,连接CD,过点B作BG⊥CD,分别交CD,CA于点E,F,与过点A且垂直于AB的直线相交于点G,连接DF,给出以下五个结论: ① ![]() ;②∠ADF=∠CDB;③点F是GE的中点;④AF=
;②∠ADF=∠CDB;③点F是GE的中点;④AF= ![]() AB;⑤S△ABC=5S△BDF ,
AB;⑤S△ABC=5S△BDF ,
其中正确结论的序号是 . 
【答案】①②④
【解析】 
解:依题意可得BC∥AG,
∴△AFG∽△BFC,∴ ![]() ,
,
又AB=BC,∴ ![]() .
.
故结论①正确;
如图,∵∠1+∠3=90°,∠1+∠4=90°,∴∠3=∠4.
在△ABG与△BCD中, ,
,
∴△ABG≌△BCD(ASA),
∴AG=BD,又BD=AD,∴AG=AD;
在△AFG与△AFD中, ,
,
∴△AFG≌△AFD(SAS),∴∠5=∠2,
又∠5+∠3=∠1+∠3=90°,∴∠5=∠1,
∴∠1=∠2,即∠ADF=∠CDB.
故结论②正确;
∵△AFG≌△AFD,∴FG=FD,又△FDE为直角三角形,∴FD>FE,
∴FG>FE,即点F不是线段GE的中点.
故结论③错误;
∵△ABC为等腰直角三角形,∴AC= ![]() AB;
AB;
∵△AFG≌△AFD,∴AG=AD= ![]() AB=
AB= ![]() BC;
BC;
∵△AFG∽△BFC,∴ ![]() ,∴FC=2AF,
,∴FC=2AF,
∴AF= ![]() AC=
AC= ![]() AB.
AB.
故结论④正确;
∵AF= ![]() AC,∴S△ABF=
AC,∴S△ABF= ![]() S△ABC;又D为中点,∴S△BDF=
S△ABC;又D为中点,∴S△BDF= ![]() S△ABF ,
S△ABF ,
∴S△BDF= ![]() S△ABC , 即S△ABC=6S△BDF .
S△ABC , 即S△ABC=6S△BDF .
故结论⑤错误.
综上所述,结论①②④正确,
故答案为:①②④.
由△AFG∽△BFC,可确定结论①正确;
由△ABG≌△BCD,△AFG≌△AFD,可确定结论②正确;
由△AFG≌△AFD可得FG=FD>FE,所以点F不是GE中点,可确定结论③错误;
由△AFG≌△AFD可得AG= ![]() AB=
AB= ![]() BC,进而由△AFG∽△BFC确定点F为AC的三等分点,可确定结论④正确;
BC,进而由△AFG∽△BFC确定点F为AC的三等分点,可确定结论④正确;
因为F为AC的三等分点,所以S△ABF= ![]() S△ABC , 又S△BDF=
S△ABC , 又S△BDF= ![]() S△ABF , 所以S△ABC=6S△BDF , 由此确定结论⑤错误.
S△ABF , 所以S△ABC=6S△BDF , 由此确定结论⑤错误.


科目:初中数学 来源: 题型:
【题目】高空抛物极其危险,是我们必须杜绝的行为.据研究,高空抛物下落的时间t(单位:s)和高度 h(单位:m)近似满足公式 t=![]() (不考虑风速的影响)
(不考虑风速的影响)
(1)从 50m 高空抛物到落地所需时间 t1 是多少 s,从 100m 高空抛物到落地所 需时间 t2 是多少 s;
(2)t2 是 t1 的多少倍?
(3)经过 1.5s,高空抛物下落的高度是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将长方形纸片ABCD对折后再展开,得到折痕EF,M是BC上一点,沿着AM再次折叠纸片,使得点B恰好落在折痕EF上的点B′处,连接AB′、BB′.

判断△AB′B的形状为 ;
若P为线段EF上一动点,当PB+PM最小时,请描述点P的位置为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明在做课本“目标与评定”中的一道题:如图1,直线a,b所成的角跑到画板外面去了,你有什么办法量出这两条直线所成的角的度数?小明的做法是:如图2,画PC∥a,量出直线b与PC的夹角度数,即直线a,b所成角的度数. 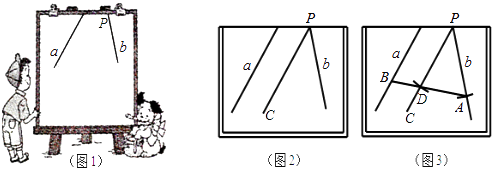
(1)请写出这种做法的理由;
(2)小明在此基础上又进行了如下操作和探究(如图3):①以P为圆心,任意长为半径画圆弧,分别交直线b,PC于点A,D;②连结AD并延长交直线a于点B,请写出图3中所有与∠PAB相等的角,并说明理由;
(3)请在图3画板内作出“直线a,b所成的跑到画板外面去的角”的平分线(画板内的部分),只要求作出图形,并保留作图痕迹.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,∠CAB=∠B=30°,AB=2 ![]() ,点D在BC边上,把△ABC沿AD翻折使AB与AC重合,得△AB′D,则△ABC与△AB′D重叠部分的面积为( )
,点D在BC边上,把△ABC沿AD翻折使AB与AC重合,得△AB′D,则△ABC与△AB′D重叠部分的面积为( ) 
A.![]()
B.![]()
C.3﹣ ![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y1=kx+b的图象与反比例函数y2= ![]() 的图象相交于点A(2,3)和点B,与x轴相交于点C(8,0).
的图象相交于点A(2,3)和点B,与x轴相交于点C(8,0). 
(1)求这两个函数的解析式;
(2)当x取何值时,y1>y2 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在10×10的网格中,每个小方格都是边长为1的小正方形,每个小正方形的顶点称为格点.若抛物线经过图中的三个格点,则以这三个格点为顶点的三角形称为抛物线的“内接格点三角形”.以O为坐标原点建立如图所示的平面直角坐标系,若抛物线与网格对角线OB的两个交点之间的距离为 ![]() ,且这两个交点与抛物线的顶点是抛物线的内接格点三角形的三个顶点,则满足上述条件且对称轴平行于y轴的抛物线条数是( )
,且这两个交点与抛物线的顶点是抛物线的内接格点三角形的三个顶点,则满足上述条件且对称轴平行于y轴的抛物线条数是( )
A.16
B.15
C.14
D.13
查看答案和解析>>
科目:初中数学 来源: 题型:
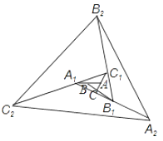
【题目】如图,△ABC面积为1,第一次操作:分别延长AB,BC,CA至点A1,B1,C1,使A1B=AB、B1C=2BC,C1A=2CA,顺次连接A1,B1,C1,得到△A1B1C1.第二次操作:分别延长A1B1,B1C1、C1A1至点A2,B2,C2,使A2B1=A1B1,B2C1=2B1C1,C2A1=2C1A1 ,顺次连接A2,B2,C2,得到△A2B2C2,…按此规律,经过2015次操作后△A2015B2015C2015的面积为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
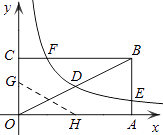
【题目】如图,矩形OABC的顶点A、C分别在x、y轴的正半轴上,点D为对角线OB的中点,点E(4,n)在边AB上,反比例函数 ![]() (k≠0)在第一象限内的图象经过点D、E,且tan∠BOA=
(k≠0)在第一象限内的图象经过点D、E,且tan∠BOA= ![]() .
.
(1)求边AB的长;
(2)求反比例函数的解析式和n的值;
(3)若反比例函数的图象与矩形的边BC交于点F,将矩形折叠,使点O与点F重合,折痕分别与x、y轴正半轴交于点H、G,求线段OG的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com