
【题目】在△ABC中,∠ACB=90°,点D、E分别在边BC、AC上,AC=3AE,∠CDE=45°(如图),△DCE沿直线DE翻折,翻折后的点C落在△ABC内部的点F,直线AF与边BC相交于点G,如果BG=AE,那么tanB=_____.

科目:初中数学 来源: 题型:
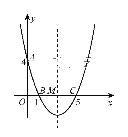
【题目】如图,在直角坐标系中,抛物线经过点A(0,4),B(1,0),C(5,0),其对称轴与x轴相交于点M.
(1)求抛物线的解析式和对称轴;
(2)在抛物线的对称轴上是否存在一点P,使△PAB的周长最小?若存在,请求出点P的坐标;若不存在,请说明理由;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:关于x的方程:mx2﹣(3m﹣1)x+2m﹣2=0.
(1)求证:无论m取何值时,方程恒有实数根;
(2)若关于x的二次函数y=mx2﹣(3m﹣1)x+2m﹣2的图象与x轴两交点间的距离为2时,求抛物线的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个圆柱体形零件,削去了占底面圆的四分之一部分的柱体(如图),现已画出了主视图与俯视图.
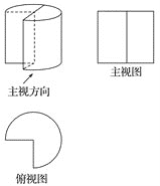
(1)请只用直尺和圆规,将此零件的左视图画在规定的位置(不必写作法,只须保留作图痕迹);
(2)若此零件底面圆的半径r=2cm,高h=3cm,求此零件的表面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC,点D为BC上一点,且AD=DC,过A,B,D三点作⊙O,AE是⊙O的直径,连结DE.
(1)求证:AC是⊙O的切线;
(2)若sinC=![]() ,AC=6,求⊙O的直径.
,AC=6,求⊙O的直径.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了解九年级学生体育测试情况,以九年级(1)班学生的体育测试成绩为样本,按A,B,C,D四个等级进行统计,并将统计结果绘制成如下的统计图,请你结合图中所给信息解答下列问题:

(说明:A级:90分~100分;B级:75分~89分;C级:60分~74分;D级:60分以下)
(1)请把条形统计图补充完整;
(2)扇形统计图中D级所在的扇形的圆心角度数是多少?
(3)若该校九年级有600名学生,请用样本估计体育测试中A级学生人数约为多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
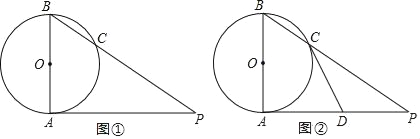
【题目】已知AB是⊙O的直径,AP是⊙O的切线,A是切点,BP与⊙O交于点C.
(1)如图①,若∠P=35°,连OC,求∠BOC的度数;
(2)如图②,若D为AP的中点,求证:直线CD是⊙O的切线.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如下图,已知⊙O的直径为AB,AC⊥AB于点A, BC与⊙O相交于点D,在AC上取一点E,使得ED=EA.下面四个结论:①ED是⊙O的切线;②BC=2OE③△BOD为等边三角形;④△EOD ∽ △CAD,正确的是( )
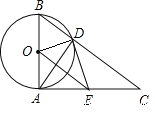
A. ①② B. ②④ C. ①②④ D. ①②③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com