�ҹ�������ѧ�һ�����˵��������ȱ��ʱ��ֱ�ۣ�������ʱ���������ν�ϰٰ�ã�����ּ������ݡ�����ѧ�У�����������������Ҫ���о���������֮������ʮ�����е���ϵ����һ�������£�������֮������ת���������
���ν�ϵĻ���˼�룬�������о�����Ĺ����У�ע��������ν���������죬��������ľ������Σ���ͼ�����ʵ�����ת��Ϊ������ϵ�����⣬���߰�������ϵ������ת��Ϊͼ�����ʵ����⣬ʹ���������������������廯������Ϊ�ף���ü�����еijɹ�������
���磺��1+2+3+4+��+n��ֵ������n����������
�������������⣬������ô������ķ�������β��ͷ�ӣ���������Ȼ���Խ��������������У����n����ż�Խ������ۣ�
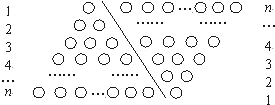
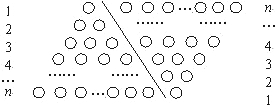
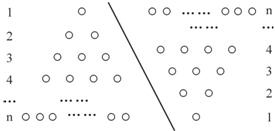
����������ν�ϵķ���������ͼ�ε�������˵��������ϵ����ʵ���Ǿͷdz���ֱ�ۣ�������ͼ�ε���������1+2+3+4+��+n��ֵ���������£���ͼ��б����ߵ�������ͼ�������ϵ���ÿ�����ηֱ�Ϊ1��2��3������n��СԲȦ������ɵģ����������������СԲȦ�ĸ���ǡΪ����ʽ��1+2+3+4+��+n��ֵ��Ϊ��ʽ�ӵ�ֵ���ְ���������ε�����б���ұߣ���ԭ���������һ��ƽ���ı��Σ���ʱ�����ƽ���ı��ε�СԲȦ����n�У�ÿ���У�n+1����СԲȦ���������ƽ���ı���СԲȦ���ܸ���Ϊn��n+1��������ˣ����һ��������СԲȦ�ĸ���Ϊ
����1+2+3+4+��+n=
��
��1�������������ν�ϵ�˼�뷽����������ͼ�Σ���1+3+5+7+��+��2n-1����ֵ������n������������Ҫ����ͼ�Σ�������ͼ������Ҫ������˵����
��2�����������һ��ͼ�Σ���1+3+5+7+��+��2n-1����ֵ������n������������Ҫ����ͼ�Σ�
������ͼ������Ҫ������˵����

 ����1+2+3+4+��+n=
����1+2+3+4+��+n= ��
�� ������ͼ������Ҫ������˵����
������ͼ������Ҫ������˵����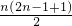 =n2��
=n2��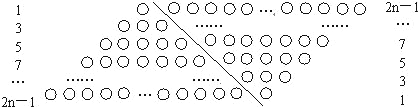



 ���ɶ���ܲ��¿�ֱͨ�п�ϵ�д�
���ɶ���ܲ��¿�ֱͨ�п�ϵ�д�
 ������ͼ������Ҫ������˵����
������ͼ������Ҫ������˵���� ���������δ�����ֵ�����ı���ʽ��
���������δ�����ֵ�����ı���ʽ�� �ҹ�������ѧ�һ�����˵���������ν�ϰٰ�ã����ѷּ����·ǣ�����ͼ����һ���߳�Ϊ1��������ֽ���ϣ������������Ϊ
�ҹ�������ѧ�һ�����˵���������ν�ϰٰ�ã����ѷּ����·ǣ�����ͼ����һ���߳�Ϊ1��������ֽ���ϣ������������Ϊ