

分析 (1)先化简,再算乘法,最后算加减;
(2)先利用二次根式的乘法计算方法计算,再进一步合并即可;
(3)首先解每个不等式,两个不等式的解集的公共部分就是不等式组的解集,然后在数轴上表示出来即可.
解答 解:(1)$\sqrt{16}$-3×$\root{3}{1-\frac{19}{27}}$-$\root{3}{-8}$
=4-3×$\frac{2}{3}$-(-2)
=4-2+2
=4;
(2)(3$\sqrt{5}$-$\sqrt{12}$)($\sqrt{45}$+2$\sqrt{3}$)-$\sqrt{1024}$
=(3$\sqrt{5}$-2$\sqrt{3}$)(3$\sqrt{5}$+2$\sqrt{3}$)-32
=45-12-32
=1;
(3)$\left\{\begin{array}{l}{2-x>0}\\{\frac{5x+1}{2}+1≥\frac{2x-1}{3}}\end{array}\right.$
解2-x>0得x<2
解$\frac{5x+1}{2}$+1≥$\frac{2x-1}{3}$得x≥-$\frac{8}{3}$x
∴不等式的解集是$-\frac{8}{3}$≤x<2
点评 此题考查二次根式的混合运算与化简求值,掌握运算顺序与解答方法是解决问题的关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:选择题
 如图,反比例反数y=$\frac{{k}_{1}}{x}$与正比例函数y=k2x的图象交于A(-2,4),B两点,若$\frac{{k}_{1}}{x}$>k2x,则x的取值范围是( )
如图,反比例反数y=$\frac{{k}_{1}}{x}$与正比例函数y=k2x的图象交于A(-2,4),B两点,若$\frac{{k}_{1}}{x}$>k2x,则x的取值范围是( )| A. | -2<x<0 | B. | -2<x<2 | C. | -2<x<0或x>2 | D. | x<-2或0<x<2 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
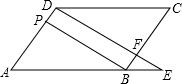 如图,在?ABCD中,F是BC上的一点,直线DF与AB的延长线相交于点E,BP∥DF,且与AD相交于点P,CD=10,AD=8,PD=2,则BE=$\frac{10}{3}$.
如图,在?ABCD中,F是BC上的一点,直线DF与AB的延长线相交于点E,BP∥DF,且与AD相交于点P,CD=10,AD=8,PD=2,则BE=$\frac{10}{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com