
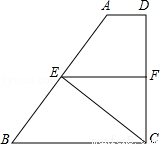
梯形ABCE中,AD∥BC,DC⊥BC,CE⊥AB于点E,点F在边CD上,且BE•CE=BC•CF.
(1)求证:AE•CF=BE•DF;
(2)若点E为AB中点,求证:AD•BC=2EC2-BC2.
(1)证明见解析;(2)证明见解析.
【解析】
试题分析:(1)求出∠B=∠DCE,证△BCE∽△CEF,推出∠BCE=∠CEF,推出EF∥BC,根据平行线分线段成比例定理得出即可.
(2)求出EF= (AD+BC),根据相似三角形的性质得出CE2=BC•EF,代入求出即可.
(AD+BC),根据相似三角形的性质得出CE2=BC•EF,代入求出即可.
试题解析:(1)∵CE⊥AB,
∴∠B+∠BCE=90°,
∵DC⊥BC,
∴∠DCE+∠BCE=90°,
∴∠B=∠DCE,
∵BE×CE=BC×CF,
∴ ,
,
∴△BCE∽△CEF,
∴∠BCE=∠CEF,
∴EF∥BC,
∴ ,
,
即AE•CF=BE•DF.
(2)∵在梯形ABCD中,EF∥BC∥AD,E为AB中点,
∴F为DC的中点,
∴EF= (AD+BC),
(AD+BC),
∵△BCE∽△CEF,
∴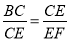 ,即CE2=BC•EF,
,即CE2=BC•EF,
∴CE2= (AD+BC)•BC,
(AD+BC)•BC,
整理得:AD•BC=2EC2-BC2.
考点:相似三角形的判定与性质.


科目:初中数学 来源:2013-2014学年上海市浦东新区中考二模数学试卷(解析版) 题型:填空题
在Rt△ABC中,∠ACB=90°,AC=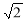 ,
,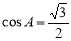 ,如果将△ABC绕着点C旋转至△A'B'C的位置,使点B' 落在∠ACB的角平分线上,A'B' 与AC相交于点H,那么线段CH的长等于 .
,如果将△ABC绕着点C旋转至△A'B'C的位置,使点B' 落在∠ACB的角平分线上,A'B' 与AC相交于点H,那么线段CH的长等于 .
查看答案和解析>>
科目:初中数学 来源:2013-2014学年上海市杨浦区5月中考二模数学试卷(解析版) 题型:填空题
如图,在菱形ABCD中,AB=a,∠ABC=α.将菱形ABCD绕点B顺时针旋转(旋转角小于90°),点A、C、D分别落在A′、C′、D′处,当A′C′⊥BC时A′D= (用含有a和α的代数式表示).
查看答案和解析>>
科目:初中数学 来源:2013-2014学年上海市杨浦区5月中考二模数学试卷(解析版) 题型:填空题
黄老师在数学课上给出了6道练习题,要求每位同学独立完成.现将答对的题目数与相应的人数列表如下:
答对题目数 | 2 | 3 | 4 | 5 | 6 |
相应的人数 | 1 | 2 | 6 | 8 | 3 |
则这些同学平均答对 道题.
查看答案和解析>>
科目:初中数学 来源:2013-2014学年上海市徐汇区中考二模数学试卷(解析版) 题型:选择题
如图,AF是∠BAC的平分线,EF∥AC交AB于点E.若∠1=25°,则∠BAF的度数为( )

A.15° B.50° C.25° D.12.5°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com