
����Ŀ����һ��ƻ�����A��B������Ṳ42����Ϊ��ҵ��Ʒ�����������ĵ��۷ֱ���50Ԫ��40Ԫ������ѧ�����������ϲ�ò�ͬ���������֪�������A����������Ҫ����B�����������![]() �����ֲ�����B�����������
�����ֲ�����B�����������![]() ���������A�����x�ᣬ����������Ṳ����yԪ��
���������A�����x�ᣬ����������Ṳ����yԪ��
��1����ƻ������������������ķ���y��Ԫ������x���ᣩ�ĺ�����ϵʽ��
��2����ί������ֲ�ͬ�Ĺ�����
��3���̵�Ϊ�˴�����������A�����ÿ������aԪ���ۣ�12��a��18����B�����ÿ������bԪ���ۣ�����ί��ͬѧ�ڸ���ʱ���֣�����������ܷ����빺��ķ����أ����ܷ�������ʱ�����ʱa��ֵ��
���𰸡���1��y��10x+1680����2����6�ֲ�ͬ�Ĺ�������3��a��18��
��������
��1����������õ�y��Ԫ������x���ᣩ�ĺ�����ϵʽ��
��2����������ɵõ�һ������x�IJ���ʽ�飬�����x��ȡֵ��Χ���ٽ�ϻ��ѵĺ���ʽ�������x�ľ�����ֵ��
��3�����ݹ���������ܷ����빺��ķ����ؿɵú�����ϵʽ��x��ϵ��Ϊ0�����ɵõ�a��b�Ĺ�ϵ���ٸ��ݺ�����С����ȷ��a��ȡֵ��Χ�����ɵõ����ۣ�
�⣺��1��������ã�y��50x+40��42��x����
��y��10x+1680��
��2���������
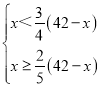 ��
��
���12��x��18��
��x��ȡ12��13��14��15��16��17��
�ʰ�ί����6�ֲ�ͬ�Ĺ�����
��3�����ܷ���Ϊw����������ã�
w��(50��a)x+(40��b) (42��x)��
w��(50��a)x+42(40��b)��(40��b)x��
w��(10��a+b��x+42(40��b)��
�߹���������ܷ����빺��ķ����أ���w��ֵ��x�أ�
��10��a+b��0��
��b��a��10��
��w��42[40��(a��10)]����42a+2100��
�ߩ�42��0����w��a�������С��
�֡�12��a��18��
��a��18ʱ��w��С��1354��Ԫ��
����a��18��


 Ӧ����㲦ϵ�д�
Ӧ����㲦ϵ�д� ״Ԫ����ϵ�д�
״Ԫ����ϵ�д� ͬ������ϵ�д�
ͬ������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڵ�����ABC�У�AB=AC=4��BC=6��D�ڵױ�BC�ϣ��ҡ�DAC=��ACD������ACD����AD����ֱ�߷��ۣ�ʹ�õ�C�䵽��E��������BE����ôBE�ij�Ϊ______.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
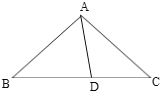
����Ŀ����12�֣���ͼ1����O��������ABCD���Խ��ߵĽ��㣬�ֱ��ӳ�OD����G��OC����E��ʹOG=2OD��OE=2OC��Ȼ����OG��OEΪ�ڱ���������OEFG������AG��DE��

��1����֤��DE��AG��
��2��������ABCD�̶�����������OEFG�Ƶ�O��ʱ����ת���ǣ�0��������360�����õ�������OE��F��G������ͼ2��
������ת�����У�����OAG����ֱ��ʱ�������Ķ�����
����������ABCD�ı߳�Ϊ1������ת�����У���AF���������ֵ�ʹ�ʱ���Ķ�����ֱ��д���������˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
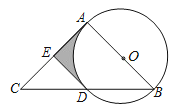
����Ŀ����ͼ��AB�ǡ�O��ֱ����AC�ǡ�O�����ߣ��е�ΪA��BC����O�ڵ�D����E��AC���е㣮
��1�����ж�ֱ��DE���O��λ�ù�ϵ����˵�����ɣ�
��2������O�İ뾶Ϊ2����B��50����AC��6����ͼ����Ӱ���ֵ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������![]() ����
����![]() ��
��![]() ���㣬������
���㣬������![]() ��һԪ���η���
��һԪ���η���![]() ��һ����Ϊ
��һ����Ϊ![]() ����
����![]() __________��
__________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ⲻ��ʽ�飺 ![]() ������������գ���ɱ���Ľⷨ��
������������գ���ɱ���Ľⷨ��
![]()
��1���ⲻ��ʽ��1������________��
��2���ⲻ��ʽ��2������________��
��3���Ѳ���ʽ ��1���� ��2���Ľ⼯�������ϱ�ʾ������
��4��ԭ����ʽ�Ľ⼯Ϊ________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABCD�У���E��F�ֱ��ڱ�AB��CD�ϣ��������������ж��ı���DEBFһ����ƽ���ı��ε��ǣ� ��

A.AE��CFB.DE��BFC.��ADE����CBFD.��AED����CFB
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������x�IJ���ʽ��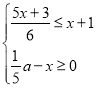 ������3�������⣬�ҹ���x�ķ�ʽ����
������3�������⣬�ҹ���x�ķ�ʽ����![]() �Ľ�Ϊ�������������������������a��ȡֵ֮��Ϊ��������
�Ľ�Ϊ�������������������������a��ȡֵ֮��Ϊ��������
A.��10B.��9C.��7D.��3
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
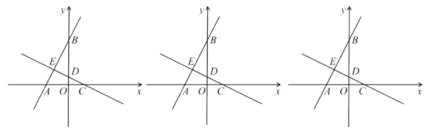
����Ŀ����֪����ͼ����ƽ��ֱ������ϵ�У���![]() Ϊ����ԭ�㣬
Ϊ����ԭ�㣬![]() ��ֱ��
��ֱ��![]() ��
��![]() �ύ�ڵ�A����
�ύ�ڵ�A����![]() ���ڵ�B����C����ֱ��AB�Ĵ��ߣ�����ΪE����
���ڵ�B����C����ֱ��AB�Ĵ��ߣ�����ΪE����![]() ���ڵ�D��
���ڵ�D��
��1����ֱ��CD�Ľ���ʽ��
��2����GΪ![]() �Ḻ������һ�㣬����EG������E��
�Ḻ������һ�㣬����EG������E��![]() ��
��![]() ���ڵ�H�����G������Ϊ
���ڵ�H�����G������Ϊ![]() ���߶�AH�ij�Ϊ
���߶�AH�ij�Ϊ![]() ����
����![]() ��
��![]() ֮��ĺ�����ϵʽ����Ҫ��д���Ա�����ȡֵ��Χ��
֮��ĺ�����ϵʽ����Ҫ��д���Ա�����ȡֵ��Χ��
��3������C��![]() ��Ĵ��ߣ�����G��
��Ĵ��ߣ�����G��![]() ��Ĵ��ߣ����߽��ڵ�M������H��
��Ĵ��ߣ����߽��ڵ�M������H��![]() �ڵ�N����ֱ��CD�ڵ�
�ڵ�N����ֱ��CD�ڵ�![]() ������MK����MKƽ��
������MK����MKƽ��![]() ����
����![]() ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com