
分析 由$\sqrt{{a}^{2}-6a+34}$+$\sqrt{{a}^{2}-2a+5}$=$\sqrt{(a-3)^{2}+{5}^{2}}$+$\sqrt{(a-1)^{2}+{2}^{2}}$,可知欲求$\sqrt{{a}^{2}-6a+34}$+$\sqrt{{a}^{2}-2a+5}$的最小值,相当于在x轴上找一点P(a,0),d到A(1,2),B(3,5)的距离之和最小.
解答 解:∵$\sqrt{{a}^{2}-6a+34}$+$\sqrt{{a}^{2}-2a+5}$=$\sqrt{(a-3)^{2}+{5}^{2}}$+$\sqrt{(a-1)^{2}+{2}^{2}}$,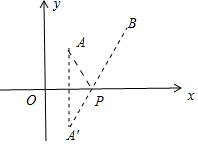
欲求$\sqrt{{a}^{2}-6a+34}$+$\sqrt{{a}^{2}-2a+5}$的最小值,相当于在x轴上找一点P(a,0),d到A(1,2),B(3,5)的距离之和最小,
作点A关于x轴的对称点A′(1,-2),连接A′B交x轴于P,点P即为所求,
易知直线A′B的解析式为y=3x-4,令y=0,解得x=$\frac{4}{3}$,
∴P($\frac{4}{3}$,0),
∴a=$\frac{4}{3}$.
故答案为$\frac{4}{3}$
点评 本题主要考查了最短路线问题,利用了数形结合的思想,通过构建一次函数求解是解题关键.


科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{5}$ | B. | $\frac{2}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
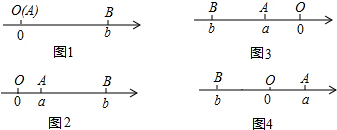
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 不变 | B. | 扩大为原来的2倍 | C. | 缩小为原来的$\frac{1}{2}$ | D. | 扩大为原来的4倍 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 售价(元/个) | 100 | 110 | 120 | 130 | … |
| 月销量(个) | 200 | 180 | 160 | 140 | … |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
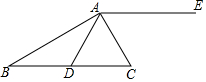 如图,在△ABC中,点D在BC边上,BD=AD=AC,AC平分∠DAE.
如图,在△ABC中,点D在BC边上,BD=AD=AC,AC平分∠DAE.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
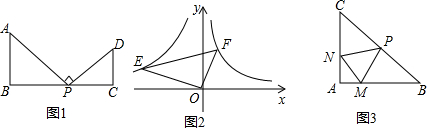
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com