
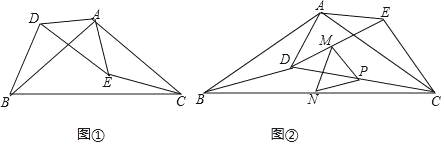
【题目】如图①,在等腰△ABC和△ADE中,AB=AC,AD=AE,且∠BAC=∠DAE=120°.
(1)求证:△ABD≌△ACE;
(2)把△ADE绕点A逆时针方向旋转到图②的位置,连接CD,点M、P、N分别为DE、DC、BC的中点,连接MN、PN、PM,判断△PMN的形状,并说明理由;
(3)在(2)中,把△ADE绕点A在平面内自由旋转,若AD=4,AB=6,请分别求出△PMN周长的最小值与最大值.
【答案】(1)证明见解析;(2)△PMN是等边三角形.理由见解析;(3)△PMN周长的最小值为3,最大值为15.
【解析】
(1)由∠BAC=∠DAE=120°,可得∠BAD=∠CAE,再由AB=AC,AD=AE,利用SAS即可判定△ABD≌△ADE;(2)△PMN是等边三角形,利用三角形的中位线定理可得PM=![]() CE,PM∥CE,PN=
CE,PM∥CE,PN=![]() BD,PN∥BD,同(1)的方法可得BD=CE,即可得PM=PN,所以△PMN是等腰三角形;再由PM∥CE,PN∥BD,根据平行线的性质可得∠DPM=∠DCE,∠PNC=∠DBC,因为∠DPN=∠DCB+∠PNC=∠DCB+∠DBC, 所以∠MPN=∠DPM+∠DPN=∠DCE+∠DCB+∠DBC=∠BCE+∠DBC=∠ACB+∠ACE+∠DBC=∠ACB+∠ABD+∠DBC=∠ACB+∠ABC,再由∠BAC=120°,可得∠ACB+∠ABC=60°,即可得∠MPN=60°,所以△PMN是等边三角形;(3)由(2)知,△PMN是等边三角形,PM=PN=
BD,PN∥BD,同(1)的方法可得BD=CE,即可得PM=PN,所以△PMN是等腰三角形;再由PM∥CE,PN∥BD,根据平行线的性质可得∠DPM=∠DCE,∠PNC=∠DBC,因为∠DPN=∠DCB+∠PNC=∠DCB+∠DBC, 所以∠MPN=∠DPM+∠DPN=∠DCE+∠DCB+∠DBC=∠BCE+∠DBC=∠ACB+∠ACE+∠DBC=∠ACB+∠ABD+∠DBC=∠ACB+∠ABC,再由∠BAC=120°,可得∠ACB+∠ABC=60°,即可得∠MPN=60°,所以△PMN是等边三角形;(3)由(2)知,△PMN是等边三角形,PM=PN=![]() BD,所以当PM最大时,△PMN周长最大,当点D在AB上时,BD最小,PM最小,求得此时BD的长,即可得△PMN周长的最小值;当点D在BA延长线上时,BD最大,PM的值最大,此时求得△PMN周长的最大值即可.
BD,所以当PM最大时,△PMN周长最大,当点D在AB上时,BD最小,PM最小,求得此时BD的长,即可得△PMN周长的最小值;当点D在BA延长线上时,BD最大,PM的值最大,此时求得△PMN周长的最大值即可.
(1)因为∠BAC=∠DAE=120°,
所以∠BAD=∠CAE,又AB=AC,AD=AE,
所以△ABD≌△ADE;
(2)△PMN是等边三角形。
理由:∵点P,M分别是CD,DE的中点,
∴PM=![]() CE,PM∥CE,
CE,PM∥CE,
∵点N,M分别是BC,DE的中点,
∴PN=![]() BD,PN∥BD,
BD,PN∥BD,
同(1)的方法可得BD=CE,
∴PM=PN,
∴△PMN是等腰三角形,
∵PM∥CE,∴∠DPM=∠DCE,
∵PN∥BD,∴∠PNC=∠DBC,
∵∠DPN=∠DCB+∠PNC=∠DCB+∠DBC,
∴∠MPN=∠DPM+∠DPN=∠DCE+∠DCB+∠DBC=∠BCE+∠DBC
=∠ACB+∠ACE+∠DBC=∠ACB+∠ABD+∠DBC=∠ACB+∠ABC,
∵∠BAC=120°,∴∠ACB+∠ABC=60°,
∴∠MPN=60°,
∴△PMN是等边三角形。
(3)由(2)知,△PMN是等边三角形,PM=PN=![]() BD,
BD,
∴PM最大时,△PMN周长最大,
∴点D在AB上时,BD最小,PM最小,
∴BD=AB-AD=2,△PMN周长的最小值为3;
点D在BA延长线上时,BD最大,PM最大,
∴BD=AB+AD=10,△PMN周长的最大值为15。
故答案为:△PMN周长的最小值为3,最大值为15


科目:初中数学 来源: 题型:
【题目】如图所示,数学家莫伦发现了世界上第一个完美长方形,它恰好能够分割成大小不同的正方形,请你完成下面计算.
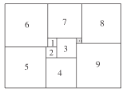
(1)如果标注1,2的正方形的边长分别是1和1.2,那么标注3的正方形的边长为________.标注5的正方形的边长为________.
(2)如果标注1,2的正方形的边长分别是![]() 和
和![]() ,求标注10的正方形的边长是多少?(用含
,求标注10的正方形的边长是多少?(用含![]() 的代数式表示)
的代数式表示)
(3)若在(2)的条件下,“勤奋小组”继续探究发现,标注9的正方形边长有两种表示方法,若标注9的正方形的边长是15,求![]() 的值?
的值?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直线l1:y=(k﹣1)x+k+1和直线l2:y=kx+k+2,其中k为不小于2的自然数.
(1)当k=2时,直线l1、l2与x轴围成的三角形的面积S2=______;
(2)当k=2、3、4,……,2018时,设直线l1、l2与x轴围成的三角形的面积分别为S2,S3,S4,……,S2018,则S2+S3+S4+……+S2018=______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点B、E分别在AC、DF上,AF分别交BD、CE于点M、N,∠A=∠F,∠1=∠2.
(1)求证:四边形BCED是平行四边形;
(2)已知DE=2,连接BN,若BN平分∠DBC,求CN的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
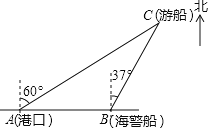
【题目】一艘观光游船从港口A以北偏东60°的方向出港观光,航行80海里至C处时发生了侧翻沉船事故,立即发出了求救信号,一艘在港口正东方向的海警船接到求救信号,测得事故船在它的北偏东37°方向,马上以40海里每小时的速度前往救援,
(1)求点C到直线AB的距离;
(2)求海警船到达事故船C处所需的大约时间.(温馨提示:sin53°≈0.8,cos53°≈0.6)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若关于x的三个方程x2+4mx+4m2+2m+3=0,x2+(2m+1)x+m2=0,(m﹣1)x2+2mx+m﹣1=0中至少有一个方程有实根,则m的取值范围是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,∠1=∠2.求证:∠3 +∠4=180°.
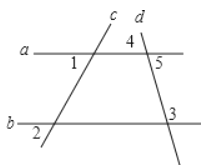
证明:∵∠1=∠2(已知)
∴ a∥b( )
∴∠3 +∠5=180° (两直线平行,同旁内角互补)
又 ∵∠4=∠5 ( )
∴∠3 +∠4=180° (等量代换)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】CD经过∠BCA顶点C的一条直线,CA=CB,E、F分别是直线CD上两点,且∠BEC=∠CFA=∠![]() ,
,
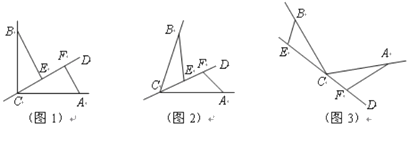
(1)若直线CD经过∠BCA的内部,且E、F在射线CD上,请解决下面两个问题:
①如图1,若∠BCA=90°,∠![]() =90°,则BE_____CF;EF____
=90°,则BE_____CF;EF____![]() .(填“>”“<”或“=”)
.(填“>”“<”或“=”)
②如图2,若0°<∠BCA<180°,请添加一个关于∠![]() 与∠BCA关系的条件__________,使①中的两个结论仍然成立,并证明两个结论成立.
与∠BCA关系的条件__________,使①中的两个结论仍然成立,并证明两个结论成立.
(2)如图3,若直线CD经过∠BCA的外部,∠![]() =∠BCA,请提出EF,BE,AF三条线段数量关系的合理猜想(不要求证明).
=∠BCA,请提出EF,BE,AF三条线段数量关系的合理猜想(不要求证明).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com