Question

如图，以Rt△ABC的直角边AB为直径的半圆O，与斜边AC交于D，E是BC边上的中点，连结DE.

(1)    DE与半圆O相切吗？若相切，请给出证明；若不相切，请说明理由；

(2)    若AD、AB的长是方程x²－10x+24=0的两个根，求直角边BC的长。

Answer 1

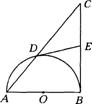
解：（1）DE与半圆O相切.    

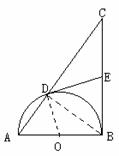      证明： 连结OD、BD     ∵AB是半圆O的直径

        ∴∠BDA=∠BDC=90° ∵在Rt△BDC中,E是BC边上的中点

∴DE=BE∴∠EBD＝∠BDE

∵OB=OD∴∠OBD=∠ODB        

又∵∠ABC＝∠OBD+∠EBD＝90°

∴∠ODB+∠EBD=90°∴DE与半圆O相切. 

  

（2）解：∵在Rt△ABC中，BD⊥AC

        ∴ Rt△ABD∽Rt△ABC  

        ∴  =  即AB²=AD·AC∴ AC=

        ∵ AD、AB的长是方程x²－10x+24=0的两个根

        ∴ 解方程x²－10x+24=0得： x­­­₁=4  x₂=6

        ∵ AD<AB  ∴ AD=4  AB=6 ∴ AC=9 

在Rt△ABC中，AB=6 AC=9

 ∴ BC===3