
【题目】如图,A、B、C三地在同一直线上,D地在A地北偏东30°方向、在C地北偏西45°方向.C地在A地北偏东75°方向.且BD=BC=30m.
(1)求∠ADC的度数;
(2)求A、D两地的距离.

【答案】(1)∠ADC的度数为75°;
(2)A、D两地的距离![]() m.
m.
【解析】试题分析:(1)过点D作DE//正北方向,则有∠ADE=30°,∠CDE=45°,这两个角相加即为∠ADC;(2)过点D作DH垂直于AC,垂足为H,求出∠DAC的度数,判断出△BCD是等边三角形,再利用三角函数求出AB的长,从而得到AB+BC+CD的长;
试题解析:
(1)过点D作DE//正北方向,如图所示:
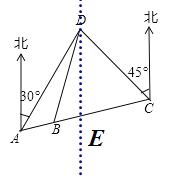
∴∠ADE=30°,∠CDE=45°,
∴∠ADC=∠ADE+∠CDE=75°;
(2)过点D作DH垂直于AC,垂足为H,如图所示:
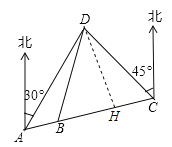
由题意可知∠DAC=75°-30°=45°,
∵△BCD是等边三角形,
∴∠DBC=60°,BD=BC=CD=30m,
∴DH=![]() ,
,
∴AD=![]() 。
。


 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案科目:初中数学 来源: 题型:
【题目】如图,某数学兴趣小组为了测量河对岸l1的两棵古树A、B之间的距离,他们在河这边沿着与AB平行的直线l2上取C、D两点,测得∠ACB=15°,∠ACD=45°,若l1、l2之间的距离为50m,则古树A、B之间的距离为m. 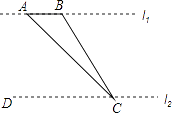
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四边形ABCD中,对角线AC,BD交于点O,下列条件中,能判定四边形ABCD为正方形的是( )
A.OA=OB=OC=OD,AB=CDB.OA=OC,OB=OD,AC⊥BD
C.OA=OB=OC=OD,AC⊥BDD.OA=OC,OB=OD,AB=BC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣x2+bx+c的顶点为Q,抛物线与x轴交于A(﹣1,0),B(5,0)两点,与y轴交于点C.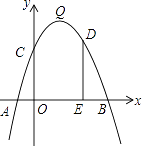
(1)求抛物线的解析式及其顶点Q的坐标;
(2)在该抛物线上求一点P,使得S△PAB=S△ABC , 求出点P的坐标:
(3)若点D是第一象限抛物线上的一个动点,过点D作DE⊥x轴,垂足为E.有一个同学说:“在第一象限抛物线上的所有点中,抛物线的顶点Q与x轴相距最远,所以当点D运动至点Q时,折线D﹣E﹣O的长度最长.”这个同学的说法正确吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
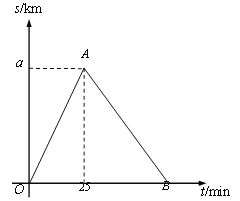
【题目】某市举行“迷你马拉松”长跑比赛,运动员从起点甲地出发,跑到乙地后,沿原路线再跑回点甲地.设该运动员离开起点甲地的路程s(km)与跑步时间t(min)之间的函数关系如图所示.已知该运动员从甲地跑到乙地时的平均速度是0.2 km/min,根据图像提供的信息,解答下列问题:
(1)a= km;
(2)组委会在距离起点甲地3km处设立一个拍摄点P,该运动员从第一次过P点到第二次过P点所用的时间为24min.
①求AB所在直线的函数表达式;
②该运动员跑完全程用时多少min?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com