
如图,已知△ABC中,∠C=90°,AC=BC,AB=6,O是BC边上的中点,N是AB边上的点(不与端点重合),M是OB边上的点,且MN∥AO,延长CA与直线MN相交于点D,G点是AB延长线上的点,且BG=AN,连接MG,设AN=x,BM=y.
(1)求y关于x的函数关系式及其定义域;
(2)连接CN,当以DN为半径的⊙D和以MG为半径的⊙M外切时,求∠ACN的正切值;
(3)当△ADN与△MBG相似时,求AN的长.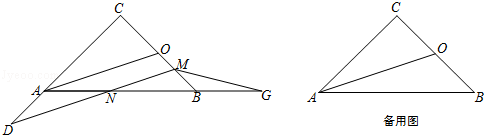
(1)y= (0<x<6) (2)tan∠ACN=
(0<x<6) (2)tan∠ACN=
(3)AN的长为2或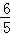
解析试题分析:(1)解:∵MN∥AO,
∴△BMN∽△BOA,
∴ =
=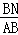 ,
,
∵∠C=90°,AC=BC,AB=6,
∴由勾股定理得:BC=3 ,
,
∵O是BC边上的中点,
∴BO= ,
,
∵AN=x,BM=y,
∴ =
= ,
,
∴y= (0<x<6);
(0<x<6);
(2)解:
∵以DN为半径的⊙D和以MG为半径的⊙M外切,
∴DN+MG=DM,又DN+MN=DM,
∴MG=MN,
∴∠MNG=∠G,
又∵∠MNG=∠AND,
∴∠AND=∠G,
∵AC=BC,
∴∠CAB=∠CBA,
∴∠DAN=∠MBG,
又∵AN=BG,
∴△AND≌△BGM,
∴DN=MG=MN,
∵∠ACB=90°,
∴CN=DN,
∴∠ACN=∠D,
∵∠ACB=90°,AC=BC,O是BC边上的中点,
∴tan∠CAO=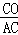 =
= ,
,
∵MN∥AO,
∴∠CAO=∠D,
∴∠CAO=∠ACN,
∴tan∠ACN= ;
;
(3)解:∵∠DAN=∠MBG,当△ADN与△MBG相似时,分为两种情况:
①若∠D=∠BMG时,过点G作GE⊥CB,垂足为点E,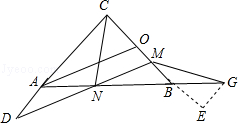
tan∠BMG= =
= ,
,
∵∠ACB=90°,GE⊥BC,
∴AC∥GE,
∴∠BGE=∠CAB=45°,
∵∠ABC=∠GBE=45°,
∴∠ABC=∠GBE=∠BGE=45°,
∴BE=EG,
∴BM=BE,
∴由勾股定理得:y= x,
x,
∵由(1)知:y=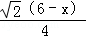 ,
,
∴解得:x=2;
②若∠D=∠G时,过点M作MF⊥AB,垂足为点F,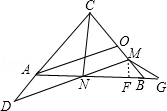
∴tan∠G=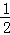 =
= ,
,
∴FG=2MF,
∵∠C=90°,AC=BC,
∴∠MBF=∠CAB=45°,
∵∠MFB=90°,
∴∠FMB=∠MBF=45°,
∴BF=MF,
∵FG=2MF=BF+BG,
∴BF=BG,
∴x=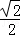 y,
y,
由(1)知:y= ,
,
∴解得:x=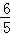 ;
;
综上所述,当△ADN与△MBG相似时,AN的长为2或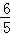 .
.
考点:相似形综合题;平行线的性质;全等三角形的判定与性质;等腰三角形的性质;勾股定理;等腰直角三角形;相似三角形的判定与性质.
点评:本题考查了相似三角形的性质和判定,全等三角形的性质和判定,平行线的性质,等腰三角形的性质,等腰直角三角形,勾股定理等知识点的运用,主要考查学生综合运用性质进行推理和计算的能力,题目综合性比较强,难度偏大,分类讨论思想的运用.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
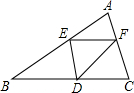 如图,已知△ABC中,BC=8,BC边上的高h=4,D为BC上一点,EF∥BC交AB于E,交AC于F(EF不过A、B),设E到BC的距离为x,△DEF的面积为y,那么y关于x的函数图象大致是( )
如图,已知△ABC中,BC=8,BC边上的高h=4,D为BC上一点,EF∥BC交AB于E,交AC于F(EF不过A、B),设E到BC的距离为x,△DEF的面积为y,那么y关于x的函数图象大致是( )查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com