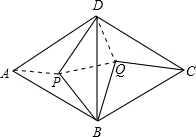
解:(1)连接DQ,当四边形BPDQ是平行四边形时,BQ=PD,
由已知,得BQ=BP,
∴BP=PD,则△BDP,△BCQ为等腰三角形,
由PD∥BQ可知,∠BDP=∠DBQ,
又∵∠BDP=∠DBP=∠CBQ,
则∠DBQ=∠CBQ,而∠DBQ+∠CBQ=60°,
∴∠BDP=∠DBP=∠CBQ=30°,
∠DPB=180°-(∠BDP+∠DBP)=120°;
(2)连接PQ,
当DP=DQ,∠PDQ=90°时,由旋转的性质可得BP=BQ,△BPQ为等边三角形,∠BPQ=60°,
∴∠BPD=∠BPQ+∠DPQ=60°+45°=105°,
当DQ=PQ,∠PQD=90°时,同理得△BPQ为等边三角形,∠BPQ=60°,
∴∠BPD=∠BPQ+∠DPQ=60°+45°=105°,
当DP=PQ,∠DPQ=90°时,同理得△BPQ为等边三角形,∠BPQ=60°,
∴∠BPD=∠BPQ+∠DPQ=60°+90°=150°;
(3)连接AP,由旋转的性质可得BP=BQ,△BPQ为等边三角形,则∠PQB=60°,
∵BD=AB,BQ=BP,∠PBQ=∠ABD=60°,
∴△BQD≌△BPA,则∠BQD=∠BPA=100°,
∴∠PQD=∠BQD-∠PQB=40°,
当PQ=PD时,∠DPQ=180°-2∠PQD=100°,∠BPD=∠BPQ+∠DPQ=100°+60°=160°,
当PQ=DQ时,∠DPQ=

(180°-40°)=70°,∠BPD=∠BPQ+∠DPQ=70°+60°=130°,
当PD=DQ时,∠DPQ=∠PQD=40°,由∠BPD=∠BPQ+∠DPQ=40°+60°=100°.
即∠BPD=160°或130°或100°.
分析:(1)当四边形BPDQ是平行四边形时,BQ=PD,由旋转的性质可知BQ=BP,则BP=PD,△BDP,△BCQ为等腰三角形,由PD∥BQ可知,∠BDP=∠DBQ,又∠BDP=∠DBP=∠CBQ,则∠DBQ=∠CBQ,而∠DBQ+∠CBQ=60°,由此可求∠PBD;
(2)连接PQ、DQ,当DP=DQ,∠PDQ=90°时,由旋转的性质可得BP=BQ,△BPQ为等边三角形,∠BPQ=60°,由∠BPD=∠BPQ+∠DPQ求解,当DQ=PQ,∠PQD=90°时,△BPQ为等边三角形,∠BPQ=60°,由∠BPD=∠BPQ+∠DPQ求解,当DP=PQ,∠DPQ=90°时,△BPQ为等边三角形,∠BPQ=60°,由∠BPD=∠BPQ+∠DPQ求解;
(3)连接AP,由旋转的性质可得BP=BQ,△BPQ为等边三角形,则∠PQB=60°,可证△BQD≌△BPA,则∠BQD=∠BPA=100°,则∠PQD=∠BQD-∠PQB=40°,根据PQ=PD,PQ=DQ,PD=DQ,分别求∠DPQ,由∠BPD=∠BPQ+∠DPQ求解.
点评:本题考查了旋转的性质,特殊三角形的性质,特殊四边形的性质.关键是利用旋转前后,对应边相等,对应角相等的性质,结合特殊三角形、四边形的性质求角.

 如图:菱形ABCD是由两个正三角形拼成的,点P在△ABD内任一点,现把△BPD绕点B旋转到△BQC的位置.则
如图:菱形ABCD是由两个正三角形拼成的,点P在△ABD内任一点,现把△BPD绕点B旋转到△BQC的位置.则 解:(1)连接DQ,当四边形BPDQ是平行四边形时,BQ=PD,
解:(1)连接DQ,当四边形BPDQ是平行四边形时,BQ=PD, (180°-40°)=70°,∠BPD=∠BPQ+∠DPQ=70°+60°=130°,
(180°-40°)=70°,∠BPD=∠BPQ+∠DPQ=70°+60°=130°,

 名校课堂系列答案
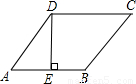
名校课堂系列答案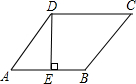 如图,菱形ABCD是周长为20cm,DE⊥AB,垂足为E,cosA=
如图,菱形ABCD是周长为20cm,DE⊥AB,垂足为E,cosA=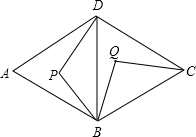 如图:菱形ABCD是由两个正三角形拼成的,点P在△ABD内任一点,现把△BPD绕点B旋转到△BQC的位置.则
如图:菱形ABCD是由两个正三角形拼成的,点P在△ABD内任一点,现把△BPD绕点B旋转到△BQC的位置.则
 ,则下列结论中:①DE=3cm;②EB=1cm;③S菱形ABCD=15cm2;④对角线AC=1.5BD.正确的个数为( )
,则下列结论中:①DE=3cm;②EB=1cm;③S菱形ABCD=15cm2;④对角线AC=1.5BD.正确的个数为( )