
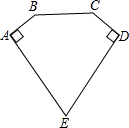
 如图,已知AE=DE=5,AB=CD,BC=4,∠E=60°,∠A=∠D=90°,那么五边形ABCDE的面积是( )
如图,已知AE=DE=5,AB=CD,BC=4,∠E=60°,∠A=∠D=90°,那么五边形ABCDE的面积是( )| A. | 6$\sqrt{2}$ | B. | 6$\sqrt{3}$ | C. | 7$\sqrt{2}$ | D. | 7$\sqrt{3}$ |
分析 作辅助线,将原五边形拓展为△EFG,证明△ABE≌△DCE(SAS),得△FEG是等边三角形,AF=DG=x,则FB=CG=2x,根据FG=EF列式可求得x的值,利用三角函数依次求FG、AB、BH的长,利用:S五边形ABCDE=S△EFG-2S△ABF代入计算即可.
解答 解:连接BE、CE,作直线BC,交ED的延长线于G,交EA的延长线于F,过E作EH⊥BC于H,
在△ABE和△DCE中,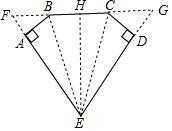
∵$\left\{\begin{array}{l}{AB=CD}\\{∠EAB=∠EDC=90°}\\{AE=DE}\end{array}\right.$,
∴△ABE≌△DCE(SAS),
∴EB=EC,∠AEB=∠DEC,
∵EH⊥BC,
∴EH平分∠BEC,
∴EF平分∠FEG,
∴△FEG是等腰三角形,
∵∠AED=60°,
∴△FEG是等边三角形,
∴EF=EG,
∴EF-AE=EG-ED,
即AF=DG,
设AF=DG=x,则FB=CG=2x,
由FG=EF得:4+4x=5+x,
x=$\frac{1}{3}$,
∴FG=4+4×$\frac{1}{3}$=$\frac{16}{3}$,
在Rt△EHG中,tan60°=$\frac{EH}{GH}=\sqrt{3}$,
∴EH=$\frac{1}{2}$×$\frac{16}{3}$×$\sqrt{3}$=$\frac{8\sqrt{3}}{3}$,
Rt△ABF中,AB=tan60°x=$\frac{\sqrt{3}}{3}$,
∴S五边形ABCDE=S△EFG-2S△ABF=$\frac{1}{2}$×$\frac{16}{3}$×$\frac{8\sqrt{3}}{3}$-2×$\frac{1}{2}$×$\frac{1}{3}$×$\frac{1}{3}$$\sqrt{3}$=7$\sqrt{3}$;
故选D.
点评 本题考查了三角形全等的性质和判定、等腰三角形、等边三角形的性质和判定、三角函数以及不规则图形面积的求法,正确做出辅助线是本题的关键,熟练掌握等边三角形的性质和判定是突破口,与直角三角形30°角的性质和特殊的三角函数相结合,使问题得以解决.


 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图ABC中,AB=AC,⊙O为△ABC的外接围,D为⊙O外一点,∠DCA=∠ACB.
如图ABC中,AB=AC,⊙O为△ABC的外接围,D为⊙O外一点,∠DCA=∠ACB.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
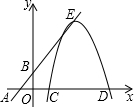 如图,一次函数y=x+2与x轴交于点A,与y轴交于点B,一抛物线的顶点在直线AB上,形状与函数y=-$\frac{1}{2}$x2图象相同,它与x轴分别交于点C、D(点C在点D的左侧),抛物线的顶点为点E.
如图,一次函数y=x+2与x轴交于点A,与y轴交于点B,一抛物线的顶点在直线AB上,形状与函数y=-$\frac{1}{2}$x2图象相同,它与x轴分别交于点C、D(点C在点D的左侧),抛物线的顶点为点E.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
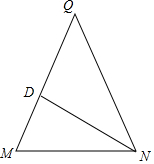 如图,在△MNQ中QM=QN,∠Q=36°,作∠QMN的平分线ND交QM于D点,求证:MN=QD=$\frac{\sqrt{5}-1}{2}$QM.
如图,在△MNQ中QM=QN,∠Q=36°,作∠QMN的平分线ND交QM于D点,求证:MN=QD=$\frac{\sqrt{5}-1}{2}$QM.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 6x6÷2x2=3x2 | B. | 8x8÷4x2=2x6 | C. | a3÷a3=0 | D. | $\frac{2}{3}$a5b÷$\frac{3}{2}$a5b=1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com