
分析 (1)将除法变为乘法,再根据乘法交换律和结合律计算即可求解;
(2)根据乘法分配律计算即可求解.
解答 解:(1)-8×(-12)×0.125×(-$\frac{1}{3}$)÷1$\frac{3}{7}$
=(-8×0.125)×[-12×(-$\frac{1}{3}$)×$\frac{7}{10}$]
=-1×$\frac{14}{5}$
=-$\frac{14}{5}$;
(2)-2.5×7.3+2.5×(-2.4)-2.5×(-1.7)
=2.5×(-7.3-2.4+1.7)
=2.5×(-10)
=-25.
点评 考查了有理数混合,关键是巧用运算律:在计算中巧妙运用加法运算律或乘法运算律往往使计算更简便.


科目:初中数学 来源: 题型:解答题
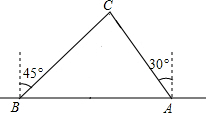 为了维护海洋权益,新组建的国家海洋局加大了在南海的巡逻力度,一天,我国两艘海监船刚好在某岛东西海岸线上的A、B两处巡逻,同时发现一艘不明国籍的船只停在C处海域,如图,在B处测得C在东北方向上,在A处测得C在北偏西30°的方向上.
为了维护海洋权益,新组建的国家海洋局加大了在南海的巡逻力度,一天,我国两艘海监船刚好在某岛东西海岸线上的A、B两处巡逻,同时发现一艘不明国籍的船只停在C处海域,如图,在B处测得C在东北方向上,在A处测得C在北偏西30°的方向上.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
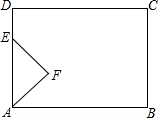 如图,在矩形ABCD中,AB=8cm,BC=6cm,动点E从点A出发.以2cm/s的速度沿射线AD方向运动,以AE为底边,在AD的右侧作等腰直角角形AEF,当点F落在射线BC上时,点E停止运动,设△AEF与矩形ABCD重叠部分的面积为S,运动的时间为t(s).
如图,在矩形ABCD中,AB=8cm,BC=6cm,动点E从点A出发.以2cm/s的速度沿射线AD方向运动,以AE为底边,在AD的右侧作等腰直角角形AEF,当点F落在射线BC上时,点E停止运动,设△AEF与矩形ABCD重叠部分的面积为S,运动的时间为t(s).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知二次函数y=x2+bx+3的图象经过点(3,0).
已知二次函数y=x2+bx+3的图象经过点(3,0).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
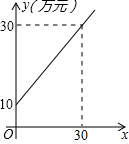 生产某种产品所需的成本y(万元)与数量x(t)之间的关系如图所示.
生产某种产品所需的成本y(万元)与数量x(t)之间的关系如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
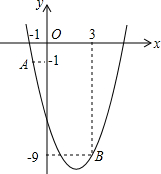 如图,已知抛物线y=ax2-4x+c的图象经过点A和点B.
如图,已知抛物线y=ax2-4x+c的图象经过点A和点B.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com