
 如图,直线y=kx+b与双曲线y=$\frac{m}{x}$交于A(x1,y1),B(x2,y2),分别与y轴,x轴交于C,D.
如图,直线y=kx+b与双曲线y=$\frac{m}{x}$交于A(x1,y1),B(x2,y2),分别与y轴,x轴交于C,D.分析 (1)根据一次函数和反比例函数的性质即可得到结论;
(2)把B(2,-1)代入y=$\frac{m}{x}$得到双曲线的解析式:y=$\frac{-2}{x}$,把A(a,4)代入y=$\frac{-2}{x}$得到直线的解析式:y=-2x+3.于是得到结论;
(3)把C(0,4),D(3,0)代入y=kx+b得到y=-$\frac{4}{3}$x+4,解方程组得到$\left\{\begin{array}{l}{{x}_{1}=\frac{3-\sqrt{8-3m}}{2}}\\{{y}_{1}=\frac{6-2\sqrt{8-3m}}{3}}\end{array}\right.$,$\left\{\begin{array}{l}{{x}_{2}=\frac{3+\sqrt{8-3m}}{2}}\\{{y}_{2}=\frac{6+\sqrt{8-3m}}{3}}\end{array}\right.$,过A作AN⊥y轴于N,过B作BM⊥x轴于M,于是得到AN=BM,CN=DM,根据全等三角形的性质得到AC=BD,根据线段的和差即可得到结论.
解答 解:(1)由一次函数有:k<0,b>0,由于双曲线在二四象限,
∴m<0,
故答案为:<,>,<;
(2)把B(2,-1)代入y=$\frac{m}{x}$得:m=2×(-1)=-2,
∴双曲线的解析式:y=$\frac{-2}{x}$,把A(a,4)代入y=$\frac{-2}{x}$得:a=$\frac{-2}{4}$=-$\frac{1}{2}$,
∴A(-$\frac{1}{2}$,4),把A(-$\frac{1}{2}$,4),B(2,-1)代入y=kx+b得:$\left\{\begin{array}{l}{-\frac{1}{2}k+b=4}\\{2k+b=-1}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=-2}\\{b=3}\end{array}\right.$,
∴直线的解析式:y=-2x+3.
当x=0,则y-3,当y=0,则x=$\frac{3}{2}$,C(0,3),D($\frac{3}{2}$,0);
(3)把C(0,4),D(3,0)代入y=kx+b得:$\left\{\begin{array}{l}{b=4}\\{3k+b=0}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{b=4}\\{k=-\frac{4}{3}}\end{array}\right.$,
∴y=-$\frac{4}{3}$x+4,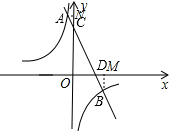
解$\left\{\begin{array}{l}{y=-\frac{4}{3}x+4}\\{y=\frac{m}{x}}\end{array}\right.$得$\left\{\begin{array}{l}{{x}_{1}=\frac{3-\sqrt{8-3m}}{2}}\\{{y}_{1}=\frac{6-2\sqrt{8-3m}}{3}}\end{array}\right.$,$\left\{\begin{array}{l}{{x}_{2}=\frac{3+\sqrt{8-3m}}{2}}\\{{y}_{2}=\frac{6+\sqrt{8-3m}}{3}}\end{array}\right.$,
过A作AN⊥y轴于N,过B作BM⊥x轴于M,
∴AN=-$\frac{3-\sqrt{8-3m}}{2}$,CN=$\frac{6-2\sqrt{8-3m}}{3}$-4=$\frac{-6-2\sqrt{8-3m}}{3}$,
∴DM=$\frac{3+\sqrt{8-3m}}{2}$-3=$\frac{-3+\sqrt{8-3m}}{2}$,BM=-($\frac{6+\sqrt{8-3m}}{3}$),
∴AN=BM,CN=DM,
∴△ACN≌△BDM,
∴AC=BD,
∴AD-BD=AD-AC=CD=$\sqrt{O{D}^{2}+O{C}^{2}}$=5.
点评 本题考查了反比例函数与一次函数交点的问题,待定系数法求函数的解析式,正确的理解题意是解题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
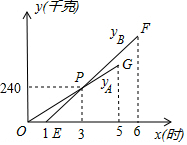 为了保证安全,某仓库引进A型、B型两台机器人搬运某种有毒货物到仓库存放,这两台机器人充满电后,各能连续工作5h,按照指令,A型机器人于某日零时开始搬运,过了1h,B型机器人也开始搬运,如图,线段OG表示A种机器人的搬运量yA(kg)与A型机器人搬运时间x(h)之间的关系图象,线段EF表示B种机器人的搬运量yB(kg)与A型机器人的时间x(h)之间的关系图象,根据图象提供的信息解答下列问题:
为了保证安全,某仓库引进A型、B型两台机器人搬运某种有毒货物到仓库存放,这两台机器人充满电后,各能连续工作5h,按照指令,A型机器人于某日零时开始搬运,过了1h,B型机器人也开始搬运,如图,线段OG表示A种机器人的搬运量yA(kg)与A型机器人搬运时间x(h)之间的关系图象,线段EF表示B种机器人的搬运量yB(kg)与A型机器人的时间x(h)之间的关系图象,根据图象提供的信息解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:填空题
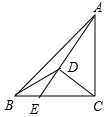 如图,在△ABC中,∠ACB=90°,D在△ABC内,DB=DC,连接AD并延长交BC于F,且AD=BC,若DE=3,BE=5,则CE的长为8.
如图,在△ABC中,∠ACB=90°,D在△ABC内,DB=DC,连接AD并延长交BC于F,且AD=BC,若DE=3,BE=5,则CE的长为8.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 种植户 | 种植A类蔬菜面积 (单位:亩) | 种植B类蔬菜面积 (单位:亩) | 总收入 (单位:元) |
| 甲 | 3 | 1 | 12500 |
| 乙 | 2 | 3 | 16500 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com