练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    3．计算：3x2•5x3．

    分析 直接利用单项式与单项式相乘，把他们的系数，相同字母分别相乘，对于只在一个单项式里含有的字母，则连同它的指数作为积的一个因式，进而得出答案．

    解答 解：3x2•5x3=15x5．

    点评 此题主要考查了单项式乘以单项式，正确掌握运算法则是解题关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    13．如图，在直角坐标系中，直线l1：y=-$\frac{1}{3}$x+1与x轴交于点C，与y轴交于点A分别以OC、OA为边作矩形ABCO，直线l2：y=x交线段AB于点E．
    （1）求点B、E的坐标；
    （2）如图，点F为线段BC的中点，点P为直线l2上一点，点Q为x轴上一点，求四边形BFQP周长的最小值以及周长最小时点P的坐标；
    （3）若点D为点A关于x轴的对称点，连接CD，将直线l1：y=-$\frac{1}{3}$x+1沿着x轴平移，平移后的直线记为l3，直线l3与x轴交于点M，与射线CD交于点N，是否存在这样的点N，使得△OMN为等腰三角形，若存在，请画出满足条件的等腰△OMN并直接写出点N的坐标；若不存在．请说明理由．

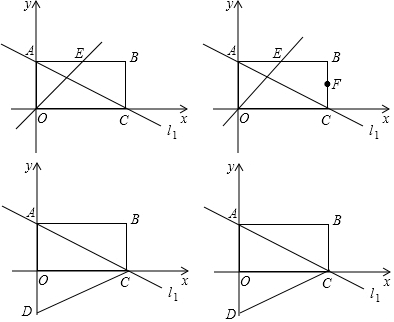
    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    14．某校八年级（1）班50名学生参加市阳光评价学业测试，全班学生的成绩统计如表：
    成绩（分）71747880828385868890919294
    人数1235453784332
    请根据表中提供的信息解答下列问题：
    （1）该班学生测试成绩的众数是88．
    （2）本次测试该班的平均分是多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

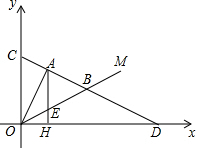    11．已知：如图三所示，在第一象限中，点A的坐标是（4，8），射线OM的解析式为y=$\frac{1}{2}$x，作线段AH⊥x轴于点H，交射线OM于点E，B在OM上，且△OAB的面积为30．
    （1）求点B的坐标；
    （2）试判断△OAB的形状，并说明理由；
    （3）如图，直线AB交坐标轴于C、D两点，若点P在线段CD上，点Q在线段OD上，且△DPQ与△OAH全等，求点P的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    18．如图1所示，已知BC∥OA，∠B=∠A=120°
    （1）说明OB∥AC成立的理由．
    （2）如图2所示，若点E，F在BC上，且∠FOC=∠AOC，OE平分∠BOF，求∠EOC的度数．
    （3）在（2）的条件下，若左右平移AC，如图3所示，那么∠OCB：∠OFB的比值是否随之发生变化？若变化，请说明理由；若不变，请求出这个比值．
    （4）在（3）的条件下，当∠OEB=∠OCA时，求∠OCA的度数．

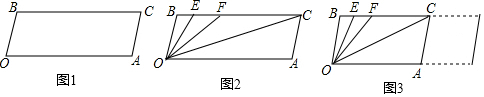
    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

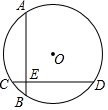    2．如图，⊙O的两条弦AB、CD互相垂直，垂足为E，且AB=CD，已知CE=1，ED=3，则⊙O的半径为（　　）
    A．$\sqrt{5}$B．$\sqrt{6}$C．$\frac{5}{2}$D．$\frac{9}{4}$

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    9．下列调查中，适合用普查方式的是（　　）
    A．了解某班学生最喜爱的体育项目B．核实某位病人血液中被感染的病毒
    C．了解长江中鱼的种类D．调查一批炮弹的杀伤半径

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    6．计算
    （1）4$\sqrt{5}$+$\sqrt{45}$-$\sqrt{8}$+4$\sqrt{2}$
    （2）（2$\sqrt{3}$+3$\sqrt{2}$）（2$\sqrt{3}$-3$\sqrt{2}$）

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    7．根据本学期“从数据谈节水”的课题学习，知道了统计调查活动要经历的5个重要步骤：①收集数据；②设计调查问卷；③用样本估计总体；④整理数据；⑤分析数据．这5个步骤的最后一步是②①④⑤③．（填序号）

    查看答案和解析>>

    同步练习册答案