
【题目】如图①,在![]() 中,
中,![]() ,
,![]() .点
.点![]() 分别是边
分别是边![]() 上的动点,连接
上的动点,连接![]() .设
.设![]() (
(![]() ),
),![]() ,
,![]() 与
与![]() 之间的函数关系如图②所示.
之间的函数关系如图②所示.
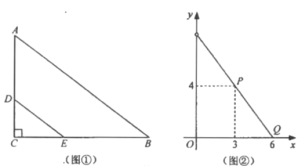
(1)求出图②中线段![]() 所在直线的函数表达式;
所在直线的函数表达式;
(2)将![]() 沿
沿![]() 翻折,得
翻折,得![]() .
.
①点![]() 是否可以落在
是否可以落在![]() 的某条角平分线上?如果可以,求出相应
的某条角平分线上?如果可以,求出相应![]() 的值;如果不可以,说明理由;
的值;如果不可以,说明理由;
②直接写出![]() 与
与![]() 重叠部分面积的最大值及相应
重叠部分面积的最大值及相应![]() 的值.
的值.
【答案】(1)![]() ;(2)①
;(2)①![]() 或
或![]() ;②
;②![]() 与
与![]() 重叠部分面积的最大值为8,此时x=4.
重叠部分面积的最大值为8,此时x=4.
【解析】
(1)利用待定系数法将(3,4)和(6,0)代入y=kx+b即可求得直线函数关系式;
(2)①根据题意可证△DCE∽△ACB,进而可得点M在CT上,且点M不在∠ACB的平分线上,接下来分类讨论,当点M在∠CAB的平分线上或在∠CBA的平分线上时,画出相应的示意图,利用角平分线定理计算即可;
②首先考虑当点M与点T重合时的x的值,进而对x分类讨论,画出相应的示意图,利用相似三角形的性质把重叠部分的面积表示出来,再利用二次函数的顶点式即可求得最大值.
解:(1)设直线PQ为y=kx+b,
将(3,4)和(6,0)代入,得
![]()
解得: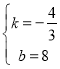
∴直线PQ为![]() ;
;
(2)①过点C作CT⊥AB,垂足为点T,
∵![]() ,
,![]()
∴在Rt△ABC中,![]() ,
,
∵![]()
∴![]()
∴![]() ,
,
∴在Rt△ACT中,![]() ,
,
∴![]() ,
,
由(1)可知![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴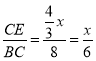 ,
,
∵![]() ,
,
∴![]() ,
,
又∵∠DCE=∠ACB,
∴△DCE∽△ACB,
∴∠DEC=∠ABC,
∴DE∥AB,
∵折叠,
∴点M在CT上,且点M不在∠ACB的平分线上,
∵![]() ,
,
∴在Rt△CDE中,![]() ,
,
∵![]()
∴![]()
∴![]()
∴![]() ,
,![]() ,
,
如图,当点M在∠CAB的平分线上时,即AM平分∠CAT,
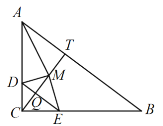
∴![]()
∴![]() ,
,
∴![]() ,
,
∴![]()
∴![]()
解得![]() ,
,
如图,当点M在∠CBA的平分线上时,即BM平分∠CBT,
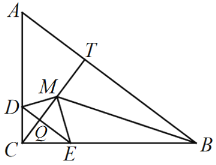
∴![]()
∴![]() ,
,
∴![]() ,
,
∴![]()
∴![]()
解得![]() ,
,
综上所述,x的值为![]() 或
或![]() ;
;
②设![]() 与
与![]() 重叠部分面积为S,
重叠部分面积为S,
如图,当点M与点T重合时,
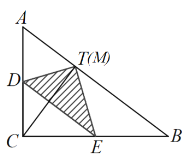
∵折叠,
∴CD=DT,
∴∠DCT=∠DTC,
∵∠ATC=90°,
∴∠DCT=∠A90°,∠DTC=∠DTA=90°,
∴∠A=∠DTA,
∴DA=DT,
∴DA=DC=![]() AC=3,
AC=3,
∴当0<x≤3时,如图,
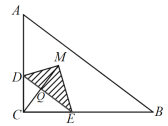
则![]()
![]()
![]()
∵0<x≤3,
∴当x=3时,S取得最大值,最大值为6,
当3<x≤6时,如图,
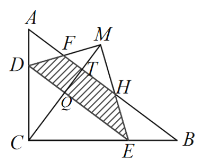
∵![]() ,
,![]()
∴![]() ,
,
∵DE∥AB,
∴![]() ,
,
∴![]() ,
,
∴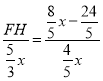 ,
,
∴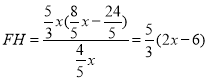 ,
,
∵![]() ,
,![]()
∴![]()
∴![]()
![]()
![]()
![]()
![]() ,
,
∴当x=4时,S取得最大值,最大值为8,
综上所述,![]() 与
与![]() 重叠部分面积的最大值为8,此时x=4.
重叠部分面积的最大值为8,此时x=4.


 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案科目:初中数学 来源: 题型:
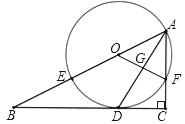
【题目】如图,在Rt△ABC中,∠C=90°,AD平分∠BAC交BC于点D,O为AB上一点,经过点A,D的⊙O分别交AB,AC于点E,F,连接OF交AD于点G.
(1)求证:BC是⊙O的切线;
(2)设AB=x,AF=y,试用含x,y的代数式表示线段AD的长;
(3)若BE=8,sinB=![]() ,求DG的长,
,求DG的长,
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是二次函数y=ax2+bx+c的图象的一部分,对称轴是直线x=1,以下结论:①abc>0;②3a+c>0;③m为任意实数,则有a(m2+1)+bm≥0;④若(﹣2,y1),(5,y2)是抛物线上的两点,则y1<y2,正确的有( )个.
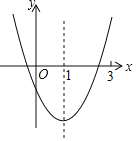
A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:有一组对边与一条对角线均相等的四边形为对等四边形,这条对角线又称对等线.
(1)如图1,在四边形ABCD中,∠C=∠BDC,E为AB的中点,DE⊥AB.求证:四边形ABCD是对等四边形.
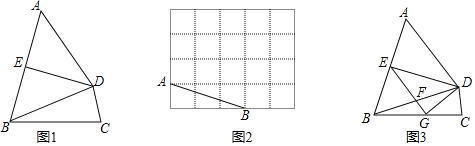
(2)如图2,在5×4的方格纸中,A,B在格点上,请画出一个符合条件的对等四边形ABCD,使BD是对等线,C,D在格点上.
(3)如图3,在图(1)的条件下,过点E作AD的平行线交BD,BC于点F,G,连结DG,若DG⊥EG,DG=2,AB=5,求对等线BD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校随机抽取部分学生就“你是否喜欢网课”进行问卷调查,并将调查结果进行统计后,绘制成如下统计表和扇形统计图.
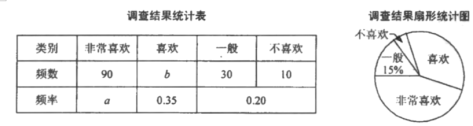
(1)在统计表中,![]() ,
,![]() ;
;
(2)求出扇形统计图中“喜欢”网课所对应扇形的圆心角度数;
(3)己知该校共有2 000名学生,试估计该校“非常喜欢”网课的学生有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为组织代表队参加市“拜炎帝、诵经典”吟诵大赛,初赛后对选手成绩进行了整理,分成5个小组(x表示成绩,单位:分),A组:75≤x<80;B组:80≤x<85;C组:85≤x<90;D组:90≤x<95;E组:95≤x<100.并绘制出如图两幅不完整的统计图.

请根据图中信息,解答下列问题:
(1)参加初赛的选手共有 名,请补全频数分布直方图;
(2)扇形统计图中,C组对应的圆心角是多少度?E组人数占参赛选手的百分比是多少?
(3)学校准备组成8人的代表队参加市级决赛,E组6名选手直接进入代表队,现要从D组中的两名男生和两名女生中,随机选取两名选手进入代表队,请用列表或画树状图的方法,求恰好选中一名男生和一名女生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)计算: ![]() +|1-
+|1-![]() |-2cos30
|-2cos30![]() +(
+(![]() )-1-(2019-
)-1-(2019-![]() )0
)0
(2)解不等式组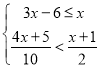 ,并求出它的整数解,再化简代数式
,并求出它的整数解,再化简代数式![]() ,从上述整数解中选择一个合适的数,求此代数式的值.
,从上述整数解中选择一个合适的数,求此代数式的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】多肉植物由于体积小、外形萌,近年来受到广大养花爱好者的青睐.创业青年小宇利用这个商机,去花卉市场选购各种多肉,了解到甲、乙、丙三种多肉的部分价格如下表.
多肉种类 价格 | 甲 | 乙 | 丙 |
批发价(元/株) |
| ||
零售价(元/株) |
|
|
|
(1)已知小宇第一次批发购进甲多肉![]() 株,乙多肉
株,乙多肉![]() 株,共花费
株,共花费![]() 元,且甲多肉每株的批发价比乙多肉低
元,且甲多肉每株的批发价比乙多肉低![]() 元,求甲多肉、乙多肉每株的批发价.
元,求甲多肉、乙多肉每株的批发价.
(2)由于销量好,第一次多肉全部售完,小宇用第一次的销售收入再批发甲、乙、丙三种多肉,且购进甲、乙多肉的株数相等,但乙多肉的批发价每株比原来降低![]() ,甲多肉的批发价,每株比原来提高
,甲多肉的批发价,每株比原来提高![]() .
.
①若他第二次批发购进甲、乙两种多肉分别花费![]() 元、
元、![]() 元,求
元,求![]() 的值.
的值.
②在![]() 的值不变的前提下,小宇把第一次的销售收入全用于第二次多肉批发,若第二次销售完这三种多肉所得利润为
的值不变的前提下,小宇把第一次的销售收入全用于第二次多肉批发,若第二次销售完这三种多肉所得利润为![]() 元,当丙多肉的株数不少于
元,当丙多肉的株数不少于![]() 时,求
时,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线![]() 与x轴交于A,B两点,点A在点B的左侧.
与x轴交于A,B两点,点A在点B的左侧.
(1)若点B的坐标为![]() .
.
①求抛物线的对称轴;
②当![]() 时,函数值y的取值范围
时,函数值y的取值范围![]() ,求n的值;
,求n的值;
(2)将抛物线在x轴上方的部分沿x轴翻折,得到新的函数图象,当![]() 时,此函数的值随x的增大而增大,直接写出m的取值范围.
时,此函数的值随x的增大而增大,直接写出m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com