
【题目】已知关于x的二次函数y=x2+(k2﹣3k﹣4)x+2k的图象与x轴从左到右交于A,B两点,且这两点关于原点对称.
(1)求k的值;
(2)在(1)的条件下,若反比例函数y=![]() 的图象与二次函数y=x2+(k2﹣3k﹣4)x+2k的图象从左到右交于Q,R,S三点,且点Q的坐标为(﹣1,﹣1),点R(xR,yR),S(xs,ys)中的纵坐标yR,ys分别是一元二次方程y2+my﹣1=0的解,求四边形AQBS的面积S四边形AQBS;
的图象与二次函数y=x2+(k2﹣3k﹣4)x+2k的图象从左到右交于Q,R,S三点,且点Q的坐标为(﹣1,﹣1),点R(xR,yR),S(xs,ys)中的纵坐标yR,ys分别是一元二次方程y2+my﹣1=0的解,求四边形AQBS的面积S四边形AQBS;
(3)在(1),(2)的条件下,在x轴下方是否存在二次函数y=x2+(k2﹣3k﹣4)x+2k图象上的点P使得S△PAB=2S△RAB?若存在,求出点P的坐标;若不存在,请说明理由.
【答案】(1)-1;(2)![]() ;(3)不存在,理由见解析
;(3)不存在,理由见解析
【解析】试题分析:(1)设A点坐标为(x1,0),B点坐标为(x2,0),由A、B两点关于原点对称,即可得x1+x2=0,又由x1+x2=﹣(k2﹣3k﹣4),即可求得k的值;
(2)由Q点的坐标求出m的值,从而确定一元二次方程y2﹣my﹣1=0即为y2+y﹣1=0,解得:y=![]() ,因为点R在点S的左边,所以yR=
,因为点R在点S的左边,所以yR=![]() ,由(1)得二次函数y=x2﹣2,令x2﹣2=0,解得:x1=-
,由(1)得二次函数y=x2﹣2,令x2﹣2=0,解得:x1=-![]() ,x2=
,x2=![]() ,所以A(﹣
,所以A(﹣![]() ,0),B(
,0),B(![]() ,0),即可求得AB的长,又由四边形AQBS的面积为:S△AQB+S△ASB求得答案;
,0),即可求得AB的长,又由四边形AQBS的面积为:S△AQB+S△ASB求得答案;
(3)由抛物线的顶点坐标为(0,﹣2),假设满足条件的点P存在,由S△PAB=2S△RAB,可得点P的纵坐标,即可得即在x轴下方抛物线上不存在点P,使S△PAB=2S△RAB.
试题解析:
(1)设A点坐标为(x1,0),B点坐标为(x2,0),
∵A、B两点关于原点对称,
∴x1+x2=0,
又x1+x2=﹣(k2﹣3k﹣4),
则k2﹣3k﹣4=0,
解得k1=﹣1,k2=4,
当k=4时,抛物线为y=x2+8,此时△=﹣32<0,舍去;
当k=﹣1时,抛物线为y=x2﹣2,此时△=8>0,则抛物线与x轴交于两点,
故所求k值为﹣1.
(2)如图:
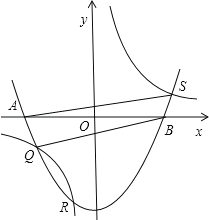
∵Q的坐标为(﹣1,﹣1),在y=![]() 上,
上,
∴-1=![]() ,
,
解得:m=1,
∴一元二次方程y2﹣my﹣1=0即为y2+y﹣1=0,
解得:y=![]() ,
,
∵点R在点S的左边,
∴yR=![]() ,
,
由(1)得二次函数y=x2﹣2,令x2﹣2=0,解得:x1=-![]() ,x2=
,x2=![]() ,
,
∴A(﹣![]() ,0),B(
,0),B(![]() ,0),
,0),
∴AB=|![]() -(-
-(-![]() )|=2
)|=2![]() ,
,
则四边形AQBS的面积为:
S△AQB+S△ASB=![]()
(3)∵抛物线的顶点坐标为(0,﹣2),假设满足条件的点P存在,
则∵S△PAB=2S△RAB,
∴点P的纵坐标为:2×(![]() )=﹣1-
)=﹣1-![]() ,
,
而﹣1﹣![]() ,
,
∴P点不存在.
即在x轴下方抛物线上不存在点P,使S△PAB=2S△RAB.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】下列命题是真命题的是( )
A.对角线互相平分的四边形是平行四边形
B.对角线相等的四边形是矩形
C.对角线互相垂直的四边形是菱形
D.对角线互相垂直的四边形是正方形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=x2+bx+c过点A(3,0),B(1,0),交y轴于点C,点P是该抛物线上一动点,点P从C点沿抛物线向A点运动(点P不与点A重合),过点P作PD∥y轴交直线AC于点D.
(1)求抛物线的解析式;
(2)求点P在运动的过程中线段PD长度的最大值;
(3)在抛物线对称轴上是否存在点M,使|MA-MC|最大?若存在,请求出点M的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程x2﹣(2k﹣2)x+k2=0有两个实数根x1,x2.
(1)求实数k的取值范围;
(2)若方程的两实数根x1,x2满足|x1+x2|=x1x2﹣22,求k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在直角坐标系中,我们把横、纵坐标都为整数的点称为整点,记顶点都是整点的三角形为整点三角形.如图,已知整点A(2,3),B(4,4),请在所给网格区域(含边界)上按要求画整点三角形.
(1)在图1中画一个△PAB,使点P的横、纵坐标之和等于点A的横坐标;
(2)在图2中画一个△PAB,使点P,B横坐标的平方和等于它们纵坐标和的4倍.


查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com