练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    先化简，再求值：（x﹣）÷，其中x=cos60°．


    解：原式=÷

    =•

    =，

    当x=cos60°=时，原式==﹣1/3．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：


    二次函数（其中），

    （1）当时，求二次函数的对称轴；

    （2）若是△的三边长，当时，二次函数最小值为，试判断△的形状，并说明理由.

    查看答案和解析>>

    科目：初中数学 来源： 题型：


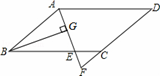
    如图，在?ABCD中，AB=6cm，AD=9cm，∠BAD的平分线交BC于点E，交DC的延长线于点F，BG⊥AE，垂足为G，BG=4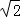cm，则EF+CF的长为　 　；



    查看答案和解析>>

    科目：初中数学 来源： 题型：


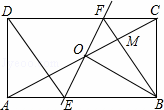
    如图，矩形ABCD中，O为AC中点，过点O的直线分别与AB，CD交于点E，F，连接BF交AC于点M，连接DE，BO．若∠COB=60°，FO=FC，则下列结论：

    ①FB⊥OC，OM=CM；

    ②△EOB≌△CMB；

    ③四边形EBFD是菱形；

    ④MB：OE=3：2．

    其中正确结论的个数是（　　）

    　

    A．

    1

    B．

    2

    C．

    3

    D．

    4

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，是由一些点组成的图形，按此规律，在第n个图形中，点的个数为　　．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，在等边△ABC中，点D在直线BC上，连接AD，作∠ADN=60°，直线DN交射线AB于点E，过点C作CF∥AB交直线DN于点F．

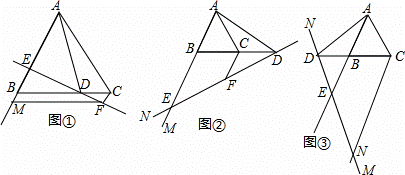
    （1）当点D在线段BC上，∠NDB为锐角时，如图①，求证：CF+BE=CD；

    （提示：过点F作FM∥BC交射线AB于点M．）

    （2）当点D在线段BC的延长线上，∠NDB为锐角时，如图②；当点D在线段CB的延长线上，∠NDB为钝角时，如图③，请分别写出线段CF，BE，CD之间的数量关系，不需要证明；

    （3）在（2）的条件下，若∠ADC=30°，S△ABC=4，则BE=　8　，CD=　4或8　．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    若一个圆锥的主视图是腰长为5，底边长为6的等腰三角形，则该圆锥的侧面积是（　　）

    　

    A．

    15π

    B．

    20π

    C．

    24π

    D．

    30π

    查看答案和解析>>

    科目：初中数学 来源： 题型：


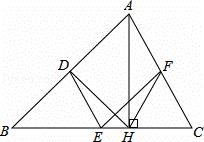
    如图，在△ABC中，点D，E，F分别是AB，BC，CA的中点，AH是边BC上的高．

    （1）求证：四边形ADEF是平行四边形；

    （2）求证：∠DHF=∠DEF．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


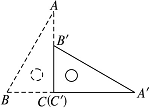
    如图，直角三角板ABC的斜边AB＝12 cm，∠A＝30°，将三角板ABC绕C顺时针旋转90°至三角板A′B′C′的位置后，再沿CB方向向左平移，使点B′落在原三角板ABC的斜边AB上，则三角板A′B′C′平移的距离为           

    查看答案和解析>>

    同步练习册答案