
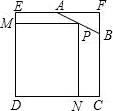
 如图,已知边长为4的正方形截去一角成为五边形ABCDE,其中AF=2,BF=1.在AB上的一点P,使得矩形PNDM有最大面积,则矩形PNDM面积的最大值是( )
如图,已知边长为4的正方形截去一角成为五边形ABCDE,其中AF=2,BF=1.在AB上的一点P,使得矩形PNDM有最大面积,则矩形PNDM面积的最大值是( )| A、8 | ||
| B、12 | ||
C、
| ||
| D、14 |
 解:延长NP交EF于G点,
解:延长NP交EF于G点,| AG |
| AF |
| PG |
| FB |
| AG |
| 2 |
| x |
| 1 |
| 3 |
| 2 |
| 25 |
| 2 |


科目:初中数学 来源: 题型:
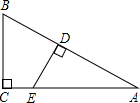 如图,Rt△ABC中,∠C=90°,∠A=30°,点D、E分别在AB、AC上,且DE⊥AB,若DE将△ABC分成面积相等的两部分,那么线段CE与AE的长度的比是
如图,Rt△ABC中,∠C=90°,∠A=30°,点D、E分别在AB、AC上,且DE⊥AB,若DE将△ABC分成面积相等的两部分,那么线段CE与AE的长度的比是查看答案和解析>>
科目:初中数学 来源: 题型:
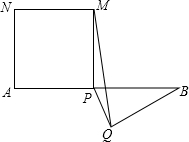 如图,P为经段AB上一点,以AP为边作一正方形APMN,以BP为底在另一侧作等腰△BPQ,连接MQ,若AB的长为4,则△MPQ的面积的最大值等于
如图,P为经段AB上一点,以AP为边作一正方形APMN,以BP为底在另一侧作等腰△BPQ,连接MQ,若AB的长为4,则△MPQ的面积的最大值等于查看答案和解析>>
科目:初中数学 来源: 题型:
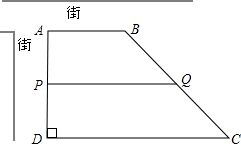 如图,现有一块梯形土地ABCD要出售,已测得上底AB=200m,高AD=230m,∠D=90°,∠C=45°.康宁房地产公司计划购买两面沿街的一块面积为25000m2的梯形地块ABQP,试求AP的长.
如图,现有一块梯形土地ABCD要出售,已测得上底AB=200m,高AD=230m,∠D=90°,∠C=45°.康宁房地产公司计划购买两面沿街的一块面积为25000m2的梯形地块ABQP,试求AP的长.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com