
【题目】已知正方形ABCD的边长为1,E为BC边的延长线上一点,CE=1,连接AE,与CD交于点F,连接BF并延长与线段DE交于点G,则BG的长为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案科目:初中数学 来源: 题型:
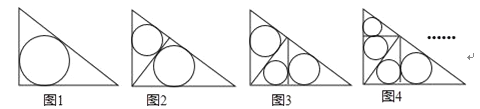
【题目】如图1~4,在直角边分别为3和4的直角三角形中,每多作一条斜边上的高就增加一个三角形的内切圆,依此类推,图10中有10个直角三角形的内切圆,它们的面积分别记为S1,S2,S3,…,S10,则S1+S2+S3+…+S10= .
查看答案和解析>>
科目:初中数学 来源: 题型:
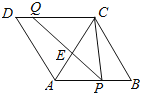
【题目】如图,菱形ABCD的边AB=8,∠B=60°,P是AB上一点,BP=3,Q是CD边上一动点,将梯形APQD沿直线PQ折叠,A的对应点为A′,当CA′的长度最小时,CQ的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
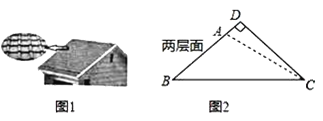
【题目】太阳能光伏建筑是现代绿色环保建筑之一,老张准备把自家屋顶改建成光伏瓦面,改建前屋顶截面△ABC如图2所示,BC=10米,∠ABC=∠ACB=36°,改建后顶点D在BA的延长线上,且∠BDC=90°,求改建后南屋面边沿增加部分AD的长.(结果精确到0.1米)
(参考数据:sin18°≈0.31,cos18°≈0.95.tan18°≈0.32,sin36°≈0.59.cos36°≈0.81,tan36°≈0.73)
查看答案和解析>>
科目:初中数学 来源: 题型:
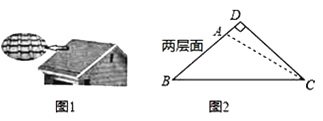
【题目】太阳能光伏建筑是现代绿色环保建筑之一,老张准备把自家屋顶改建成光伏瓦面,改建前屋顶截面△ABC如图2所示,BC=10米,∠ABC=∠ACB=36°,改建后顶点D在BA的延长线上,且∠BDC=90°,求改建后南屋面边沿增加部分AD的长.(结果精确到0.1米)
(参考数据:sin18°≈0.31,cos18°≈0.95.tan18°≈0.32,sin36°≈0.59.cos36°≈0.81,tan36°≈0.73)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如今很多初中生喜欢购头饮品饮用,既影响身体健康又给家庭增加不必要的开销,为此某班数学兴趣小组对本班同学一天饮用饮品的情况进行了调查,大致可分为四种:A.白开水,B.瓶装矿泉水,C.碳酸饮料,D.非碳酸饮料.根据统计结果绘制如下两个统计图,根据统计图提供的信息,解答下列问题
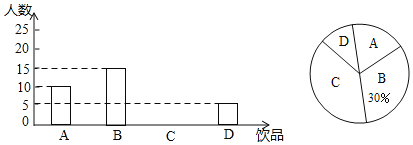
(1)这个班级有多少名同学?并补全条形统计图;
(2)若该班同学每人每天只饮用一种饮品(每种仅限一瓶,价格如下表),则该班同学每天用于饮品的人均花费是多少元?
饮品名称 | 白开水 | 瓶装矿泉水 | 碳酸饮料 | 非碳酸饮料 |
平均价格(元/瓶) | 0 | 2 | 3 | 4 |
(3)为了养成良好的生活习惯,班主任决定在饮用白开水的5名班委干部(其中有两位班长记为A,B,其余三位记为C,D,E)中随机抽取2名班委干部作良好习惯监督员,请用列表法或画树状图的方法求出恰好抽到2名班长的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
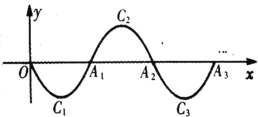
【题目】如图,二次函数![]() 的图象记为
的图象记为![]() ,它与
,它与![]() 轴交于点
轴交于点![]() ,
,![]() ;将
;将![]() 绕点
绕点![]() 旋转180°得
旋转180°得![]() ,交
,交![]() 轴于点
轴于点![]() ;将
;将![]() 绕点
绕点![]() 旋转180°得
旋转180°得![]() ,交
,交![]() 轴于点
轴于点![]() ;……如此进行下去,得到一条“波浪线”.若
;……如此进行下去,得到一条“波浪线”.若![]() 在这条“波浪线”上,则
在这条“波浪线”上,则![]() ____.
____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在⊿OAB中,∠OAB=90°.OA=AB=6.将⊿OAB绕点O逆时针方向旋转90°得到⊿OA1B1

(1)线段A1B1的长是 ∠AOA1的度数是
(2)连结AA1,求证:四边形OAA1B1是平行四边形 ;
(3)求四边形OAA1B1的面积 .
查看答案和解析>>
科目:初中数学 来源: 题型:
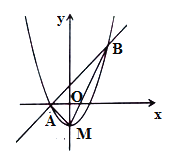
【题目】如图,抛物线![]() 的顶点为
的顶点为![]() ,且抛物线与直线
,且抛物线与直线![]() 相交于
相交于![]() 两点,且点
两点,且点![]() 在
在![]() 轴上,点
轴上,点![]() 的坐标为
的坐标为![]() ,连接
,连接![]() .
.
(1)![]() ,
,![]() ,
,![]() (直接写出结果);
(直接写出结果);
(2)当![]() 时,则
时,则![]() 的取值范围为 (直接写出结果);
的取值范围为 (直接写出结果);
(3)在直线![]() 下方的抛物线上是否存在一点
下方的抛物线上是否存在一点![]() ,使得
,使得![]() 的面积最大?若存在,求出
的面积最大?若存在,求出![]() 的最大面积及点
的最大面积及点![]() 坐标.
坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com