练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    已知：已知二次函数的图象对称轴为，且过点B（－1，0）．求此二次函数的表达式.

    ．

    解析试题分析：先根据抛物线的对称轴方程得到-=2，解得a=-1，然后把B点坐标代入y=-x2+4x+c，求出c的值即可．
    试题解析:∵此二次函数图象的对称轴为
    ∴
    解得：
    ∴此二次函数的表达式为
    ∵点B（-1，0）在此函数图象上，
    ∴
    解得：
    ∴此二次函数的表达式为
    考点: 待定系数法求二次函数解析式.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    如图,等边△ABC的边长为4,E是边BC上的动点,EH⊥AC于H,过E作EF∥AC,交线段AB于点F,在线段AC上取点P,使PE＝EB．设EC＝x（0＜x≤2）．

    （1）请直接写出图中与线段EF相等的两条线段（不再另外添加辅助线）；
    （2）Q是线段AC上的动点,当四边形EFPQ是平行四边形时,求平行四边形EFPQ的面积（用含的代数式表示）；
    （3）当（2）中 的平行四边形EFPQ面积最大值时,以E为圆心,r为半径作圆,根据⊙E与此时平行四边形EFPQ四条边交点的总个数,求相应的r的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    如图，在平面直角坐标系xOy中，边长为2的正方形OABC的顶点A、C分别在x轴、y轴的正半轴上，二次函数y=-x2+bx+c的图象经过B、C两点．

    （1）求b，c的值．
    （2）结合函数的图象探索：当y＞0时x的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    已知抛物线y=x2+bx+c经过（2，－1）和（4,3）两点．
    (1)求出这个抛物线的解析式；
    (2)将该抛物线向右平移1个单位，再向下平移3个单位，得到的新抛物线解析式为             .

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    如图，二次函数的图象与一次函数的图象交于，两点. C为二次函数图象的顶点.

    （1）求二次函数的解析式；
    （2）定义函数f：“当自变量x任取一值时，x对应的函数值分别为y1或y2，若y1≠y2，函数f的函数值等于y1、y2中的较小值;若y1=y2，函数f的函数值等于y1（或y2）.” 当直线（k >0）与函数f的图象只有两个交点时，求的值.

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    已知函数y=mx2－6x＋1（m是常数）．
    ⑴求证：不论m为何值，该函数的图象都经过y轴上的一个定点；
    ⑵若该函数的图象与x轴只有一个交点，求m的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    已知：抛物线与x轴交于点A、B（A左B右），其中点B的坐标为（7，0），设抛物线的顶点为C．

    （1）求抛物线的解析式和点C的坐标；
    （2）如图1，若AC交y轴于点D，过D点作DE∥AB交BC于E．点P为DE上一动点，PF⊥AC于F，PG⊥BC于G．设点P的横坐标为a，四边形CFPG的面积为y，求y与a的函数关系式和y的最大值；
    （3）如图2，在条件（2）下，过P作PH⊥x轴于点H，连结FH、GH，是否存在点P，使得△PFH与△PHG相似？若存在，求出P点坐标；若不存在，说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    某汽车租赁公司拥有20辆汽车．据统计，当每辆车的日租金为400元时，可全部租出；当未租出的车将增加1辆,每辆车的日租金每增加50元，；公司平均每日的各项支出共4800元．设公司每日租出工辆车时，日收益为y元．（日收益=日租金收入一平均每日各项支出）
    （1）公司每日租出x辆车时，每辆车的日租金为　    　元（用含x的代数式表示）；
    （2）当每日租出多少辆时，租赁公司日收益最大？最大是多少元？
    （3）当每日租出多少辆时，租赁公司的日收益不盈也不亏？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    某商品的进价为每件40元，售价为每件50元，每个月可卖出210件；如果每件商品的售价每上涨1元，则每个月少卖10件（每件售价不能高于65元）．
    设每件商品的售价上涨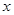元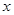（为正整数），每个月的销售利润为元．
    （1）求与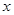的函数关系式并直接写出自变量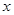的取值范围；
    （2）每件商品的售价定为多少元时，每个月可获得最大利润？最大的月利润是多少元？
    （3）每件商品的售价定为多少元时，每个月的利润恰为2200元？根据以上结论，请你直接写出售价在什么范围时，每个月的利润不低于2200元？

    查看答案和解析>>

    同步练习册答案