
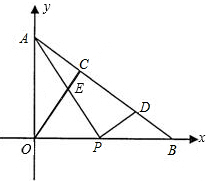
 在平面直角坐标中,Rt△OAB的两顶点A,B分别在y轴,x轴的正半轴上,点O是原点.其中点A(0,3),B(4,0),OC是Rt△OAB的高,点P以每秒1个单位长的速度在线段OB上由点O向点B运动(与端点不重合),过点P作PD⊥AP交AB于点D,设运动时间为t秒.
在平面直角坐标中,Rt△OAB的两顶点A,B分别在y轴,x轴的正半轴上,点O是原点.其中点A(0,3),B(4,0),OC是Rt△OAB的高,点P以每秒1个单位长的速度在线段OB上由点O向点B运动(与端点不重合),过点P作PD⊥AP交AB于点D,设运动时间为t秒. ,求点E的坐标;
,求点E的坐标;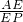 的值.
的值. ,OA=3,
,OA=3, ,即
,即 ,所以OF=
,所以OF= ,
, ).
).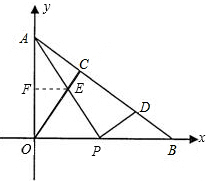 ∠AEO=∠PDB=90°+∠PAB,
∠AEO=∠PDB=90°+∠PAB, ;
; ,即
,即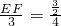 ,所以EF=
,所以EF=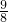 ,
, ,即
,即 ,所以t=
,所以t= ,
, ;
; .
. ,仿照(1)的方法,可通过△OEF∽△BAO,求得EF的长,而△AEF∽△APO,根据相似三角形所得比例线段即可求得OP的长即t的值.
,仿照(1)的方法,可通过△OEF∽△BAO,求得EF的长,而△AEF∽△APO,根据相似三角形所得比例线段即可求得OP的长即t的值. ;由(2)证得△AOE∽△PBD,那么AE:PD=OA:PB,由于OA=3,PB=OB-OP=1,因此AE=3PD,可设PD=x,则AE=3x,易得△AEC∽△ADP,则有:
;由(2)证得△AOE∽△PBD,那么AE:PD=OA:PB,由于OA=3,PB=OB-OP=1,因此AE=3PD,可设PD=x,则AE=3x,易得△AEC∽△ADP,则有: ,根据射影定理可在Rt△ABO中求出AC的长,利用勾股定理可求得EC的表达式,将它们代入上式比例式中,即可求得x的值,进而可得到EC、AE的长,有了AE、AP的长,即可得到AE:EP的值.
,根据射影定理可在Rt△ABO中求出AC的长,利用勾股定理可求得EC的表达式,将它们代入上式比例式中,即可求得x的值,进而可得到EC、AE的长,有了AE、AP的长,即可得到AE:EP的值.

科目:初中数学 来源: 题型:
 22、如图所示,在平面直角坐标中,抛物线的顶点P到轴的距离是4,抛物线与x轴相交于O、M两点,OM=4;矩形ABCD的边BC在线段的OM上,点A、D在抛物线上.
22、如图所示,在平面直角坐标中,抛物线的顶点P到轴的距离是4,抛物线与x轴相交于O、M两点,OM=4;矩形ABCD的边BC在线段的OM上,点A、D在抛物线上.查看答案和解析>>
科目:初中数学 来源: 题型:
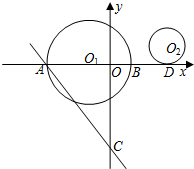 在平面直角坐标中,点O1(-4,0),半径为8的⊙O1与x轴交于A、B,过A作直线l与x轴负方向成60°角,且交y轴于点C,以点O2(13,5)为圆心的圆与x轴切于点D.
在平面直角坐标中,点O1(-4,0),半径为8的⊙O1与x轴交于A、B,过A作直线l与x轴负方向成60°角,且交y轴于点C,以点O2(13,5)为圆心的圆与x轴切于点D.查看答案和解析>>
科目:初中数学 来源: 题型:
 ∠COA=45°,动点P从点O出发,在梯形OABC的边上运动,路径为O→A→B→C,到达点C时停止.作直线CP.
∠COA=45°,动点P从点O出发,在梯形OABC的边上运动,路径为O→A→B→C,到达点C时停止.作直线CP.查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com