
【题目】(1)如图①,已知:在△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥直线m, CE⊥直线m,垂足分别为点D、E.证明:DE=BD+CE.
(2)如图②,将(1)中的条件改为:在△ABC中,AB=AC,D、A、E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC=α,其中α为任意钝角.请问结论DE=BD+CE是否成立?如成立,请你给出证明;若不成立,请说明理由.

【答案】(1)证明详见解析;(2)结论DE=BD+CE仍然成立,证明详见解析.
【解析】试题分析:(1)、根据BD⊥直线m,CE⊥直线m得出∠BDA=∠AEC=90°,然后根据∠BAC=90°得出∠DBA=∠EAC,从而说明△ABD和△CAE全等,得出BD=AE,AD=CE,从而得出答案;(2)、根据∠BDA=α得出∠DBA+∠BAD=180°-α,根据∠BAC =α得出∠BAD+∠EAC=180°-α,从而说明∠DBA =∠EAC,然后得出△ABD和△CAE全等,从而得出BD=AE,AD=CE,然后得出答案.
试题解析:(1)、∵BD⊥直线m,CE⊥直线m,垂足分别为D、E ∴∠BDA=∠AEC=90°
∴∠DBA+∠BAD=90° ∵∠BAC=90° ∴∠BAD+∠EAC=90° ∴∠DBA=∠EAC
在△ABD与△CAE中 ∵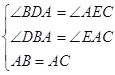 ∴△ABD≌△CAE
∴△ABD≌△CAE
∴BD=AE,AD=CE ∴DE=AD+AE=CE+BD
(2)、结论DE=BD+CE成立
在△ABD中,∵∠BDA=α ∴∠DBA+∠BAD=180°-α ∵∠BAC =α ∴∠BAD+∠EAC=180°-α
∴∠DBA =∠EAC
在△ABD与△CAE中,∵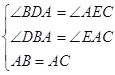 ∴△ABD≌△CAE ∴BD=AE,AD=CE ∴DE=AD+AE=CE+BD
∴△ABD≌△CAE ∴BD=AE,AD=CE ∴DE=AD+AE=CE+BD


科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线l:y=![]() x+1交x轴于点A,交y轴于点B,点A1、A2、A3,…在x轴的正半轴上,点B1、B2、B3,…在直线l上.若△OB1A1,△A1B2A2,△A2B3A3,…均为等边三角形,则△A6B7A7的周长是_____.
x+1交x轴于点A,交y轴于点B,点A1、A2、A3,…在x轴的正半轴上,点B1、B2、B3,…在直线l上.若△OB1A1,△A1B2A2,△A2B3A3,…均为等边三角形,则△A6B7A7的周长是_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,正方形ABCD的边长为6,菱形EFGH的三个顶点E、G、H 分别在正方形ABCD边AB、CD、DA上,AH=2.
(1)如图1,当DG=2,且点F在边BC上时.
求证:① △AHE≌△DGH;
② 菱形EFGH是正方形;
(2)如图2,当点F在正方形ABCD的外部时,连接CF.
① 探究:点F到直线CD的距离是否发生变化?并说明理由;
② 设DG=x,△FCG的面积为S,是否存在x的值,使得S=1,若存在,求出x的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等腰直角三角形ABC中,∠ACB=90°,AC=BC=4,D是AB的中点,E,F分别是AC,BC上的点(点E不与端点A,C重合),且AE=CF,连接EF并取EF的中点O,连接DO并延长至点G,使GO=OD,连接DE,DF,GE,GF. 
(1)求证:四边形EDFG是正方形;
(2)当点E在什么位置时,四边形EDFG的面积最小?并求四边形EDFG面积的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC内接于O,AB=AC,D在劣弧AC上,∠ABD=45°
(1) 如图1,BD交AC于E,连CD.若AB=BD,求证:CD=![]() DE
DE
(2) 如图2,连AD、CD,已知sin∠BDC=![]() ,求tan∠CBD的值
,求tan∠CBD的值


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC,D是BC的中点,AC的垂直平分线分别交AC,AD,AB于点E,O,F,则图中全等三角形的对数是( ) 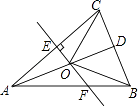
A.1对
B.2对
C.3对
D.4对
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com