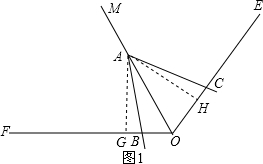
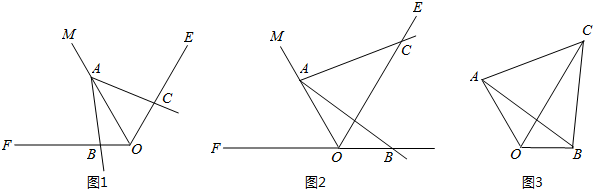
(1)证明:过A作AG⊥OF于G,AH⊥OE于H,
则∠AHO=∠AGO=90°,
∵∠EOF=120°,
∴∠HAG=60°=∠BAC,
∴∠HAG-∠BAH=∠BAC-∠BAH,
∴∠BAG=∠CAH,
∵OM平分∠EOF,AG⊥OF,AH⊥OE,
∴AG=AH,
在△BAG和△CAH中,
∵
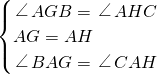
,
∴△BAG≌△CAH(ASA),
∴AB=AC;
(2)结论还成立,
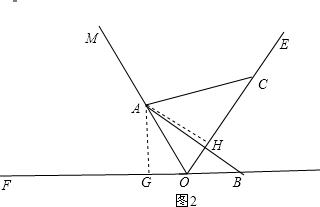
证明:过A作AG⊥OF于G,AH⊥OE于H,
与(1)证法类似根据ASA证△BAG≌△CAH(ASA),
则AB=AC;
(3)证明:①如图,∠FOA=180°-120°=60°,
∠FOC=60°+60°=120°,
即OM平分∠COF,
由(2)知:AC=AB,
∵∠CAB=60°,
∴△ABC是等边三角形;

②在OC上截取BO=ON,连接BN,
∵∠COB=60°,
∴△BON是等边三角形,
∴ON=OB,∠OBN=60°,
∵△ABC是等边三角形,
∴∠ABC=60°=∠NBO,
∴都减去∠ABN得:∠ABO=∠CBN,
在△AOB和△CNB中
∵
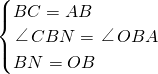
,
∴△AOB≌△CNB(SAS),
∴NC=OA,
∴OC=ON+CN=OB+OA,
即OC=OA+OB.
分析:(1)过A作AG⊥OF于G,AH⊥OE于H,求出∠CAH=∠BAG,根据ASA证△BAG≌△CAH,推出AB=AC即可;
(2)证法与(1)类似,过A作AG⊥OF于G,AH⊥OE于H,求出∠CAH=∠BAG,根据ASA证△BAG≌△CAH,推出AB=AC即可;
(3)①还原图形与图2类似由(2)知AC=AB,∠CAB=60°,根据等边三角形的判定推出即可;
②在OC上截取BO=ON,连接NB,得出等边三角形BON,求出∠ABO=∠CBN,证△AOB≌△CNB,推出NC=OA即可.
点评:本题考查了等边三角形的性质和判定,全等三角形的性质和判定,主要考查学生综合运用性质进行推理的能力,题目比较典型,证明过程类似,是一道探究性的题目.

 (1)证明:过A作AG⊥OF于G,AH⊥OE于H,
(1)证明:过A作AG⊥OF于G,AH⊥OE于H,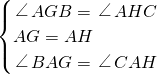 ,
,
 ②在OC上截取BO=ON,连接BN,
②在OC上截取BO=ON,连接BN,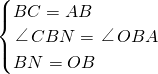 ,
,

 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案 下列说法:
下列说法:


