
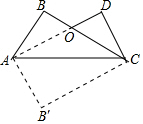
 把长方形AB′CD沿对角线AC折叠,得到如图所示的图形,已知∠BAO=30°,
把长方形AB′CD沿对角线AC折叠,得到如图所示的图形,已知∠BAO=30°,分析 (1)先依据翻折的性质得到∠B=90°,然后可求得∠BOA=60°,依据邻补角的性质可求得∠AOC的度数,然后依据翻折的性质和平行线的性质可证明∠2=∠3=30°,然后可求得∠BAC的度数;
(2)先求得OA的长度,然后依据AO=OC可求得OC的长,最后在Rt△ODC中,依据勾股定理可求得DC的长
解答 (1)解:∵四边形AB'CD是矩形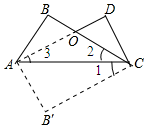
∴AD∥B'C,∠B'=900
∴∠1=∠3,
∵翻折后∠1=∠2,
∴∠2=∠3.
∵翻折后∠B=∠B'=90°,∠BAO=30°,
∴∠AOC=∠B+∠BAO=120°,
∴∠2=∠3=30°,
∴∠BAC=∠BAO+∠3=60°,
答:∠AOC为120°,∠BAC为60°.
(2)∵∠2=∠3,
∴AO=CO,AD=$3\sqrt{3}$,OD=$\sqrt{3}$
∴AO=CO=$2\sqrt{3}$,
∵四边形AB'CD是矩形,
∴∠D是直角.
∴在Rt△ODC中,$CD=\sqrt{O{C^2}-O{D^2}}=\sqrt{{{({2\sqrt{3}})}^2}-{{({\sqrt{3}})}^2}}=3$.
答:CD长3.
点评 本题主要考查的是翻折的性质、矩形的性质、勾股定理的应用,证得∠3=∠2是解题的关键.


 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:初中数学 来源: 题型:解答题
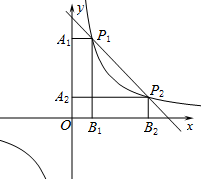 如图,已知点P1(2,8)在反比例函数y1=$\frac{m}{x}$的图象上,一次函数y2=kx+t的图象经过点P1,并与反比例函数y1=$\frac{m}{x}$的图象交于第一象限的点P2(a,b).
如图,已知点P1(2,8)在反比例函数y1=$\frac{m}{x}$的图象上,一次函数y2=kx+t的图象经过点P1,并与反比例函数y1=$\frac{m}{x}$的图象交于第一象限的点P2(a,b).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3-(2-3)=2 | B. | 2(2a-b)-3(b-2a)=10a-5b | ||
| C. | 6÷($\frac{1}{2}$-$\frac{1}{3}$)=12-18=-6 | D. | (-4)2-$\root{3}{-8}$=14 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 在平面内,两条互相垂直、原点重合的数轴的垂足是原点 | |
| B. | 平面直角坐标系所在平面叫坐标平面 | |
| C. | 坐标平面上的点与有序数对是一一对应的 | |
| D. | 凡是两条互相垂直的直线都能组成平面直角坐标系 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com