
| A. | (-2,3) | B. | (2,3) | C. | (3,-2) | D. | (3,2) |
科目:初中数学 来源: 题型:解答题
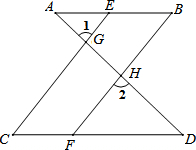 完成下面推理过程:
完成下面推理过程:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
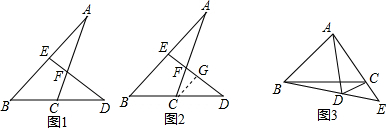
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
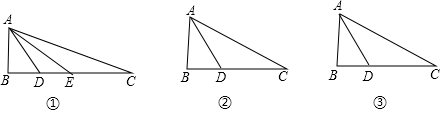
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
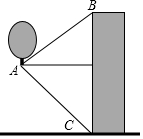 热气球的探测器显示,从热气球底部A处看一栋高楼顶部B的仰角为30°,看这栋楼底部C的俯角为45°,已知楼高是120m,热气球若要飞越高楼,问至少要继续上升多少米?(结果保留根号)
热气球的探测器显示,从热气球底部A处看一栋高楼顶部B的仰角为30°,看这栋楼底部C的俯角为45°,已知楼高是120m,热气球若要飞越高楼,问至少要继续上升多少米?(结果保留根号)查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 5 | B. | 3 | C. | 1 | D. | 0 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
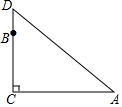 如图,有一个三角形花圃,∠C=90°,AC=20m,BC=10m,两个人同时从点B处出发,以相同速度沿着花圃四周散步,一个沿着BD,DA方向走,另一个沿着BC,CA方向走,结果他们在点A处首次相遇,你能据此求出AD的长吗?试试看.
如图,有一个三角形花圃,∠C=90°,AC=20m,BC=10m,两个人同时从点B处出发,以相同速度沿着花圃四周散步,一个沿着BD,DA方向走,另一个沿着BC,CA方向走,结果他们在点A处首次相遇,你能据此求出AD的长吗?试试看.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1562 | B. | 1806 | C. | 3367 | D. | 3369 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com