
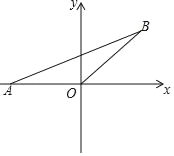
【题目】如图,等腰△AOB中,AO=BO=2,点A在x轴上,OB与x轴的夹角为45°;
(1)求直线AB、OB的解析式;
(2)若将△AOB沿着x轴翻折再向右平移两个单位求直线AB的解析式.
【答案】(1)直线AB的解析式为:y=(![]() ﹣1)x+2
﹣1)x+2![]() +1,直线OB的解析式为y=x;(2)y=﹣(1+
+1,直线OB的解析式为y=x;(2)y=﹣(1+![]() )x.
)x.
【解析】
(1)过B作BC⊥x轴于C,根据已知条件得到BC=OC,求得A(-2,0),B(![]() ,
,![]() ),解方程组即可得到结论;
),解方程组即可得到结论;
(2)根据折叠的性质得到点B的对称点为B′(![]() ,-
,-![]() ),向右平移两个单位,得到点A的对称点为A′(0,0),点B′的对称点B″(
),向右平移两个单位,得到点A的对称点为A′(0,0),点B′的对称点B″(![]() +2,-
+2,-![]() ),解方程组即可得到结论.
),解方程组即可得到结论.
(1)过B作BC⊥x轴于c,
∵∠BOC=45°,
∴BC=OC,
∵AO=BO=2,
∴BC=OC=![]() ,
,
∴A(﹣2,0),B(![]() ,
,![]() ),
),
设直线AB的解析式为:y=kx+b,
∴![]() ,
,
解得:![]() ,
,
∴直线AB的解析式为:y=(![]() ﹣1)x+2
﹣1)x+2![]() +1,
+1,
设直线OB的解析式为y=mx,
∴![]() =
=![]() m,
m,
∴m=1,
∴直线OB的解析式为y=x;
(2)∵将△AOB沿着x轴翻折,
∴点B的对称点为B′(![]() ,﹣
,﹣![]() ),
),
∵再向右平移两个单位,
∴点A的对称点为A′(0,0),点B′的对称点B″(![]() +2,﹣
+2,﹣![]() ),
),
设平移后的直线的解析式为:y=ax,
∴﹣![]() =(
=(![]() +2)a,
+2)a,
∴a=﹣(1+![]() ),
),
∴将△AOB沿着x轴翻折再向右平移两个单位求直线AB的解析式为y=﹣(1+![]() )x.
)x.


 小学教材完全解读系列答案
小学教材完全解读系列答案科目:初中数学 来源: 题型:
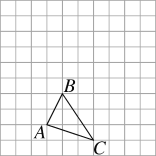
【题目】如图,已知单位长度为1的方格中有三角形ABC.
(1)请画出三角形ABC向上平移3格再向右平移2格所得的三角形A′B′C′;
(2)请以点A为坐标原点建立平面直角坐标系(在图中画出),然后写出点B,B′的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为 ![]() 的正方形ABCD中,动点F,E分别以相同的速度从D,C两点同时出发向C和B运动(任何一个点到达即停止),在运动过程中,则线段CP的最小值为 .
的正方形ABCD中,动点F,E分别以相同的速度从D,C两点同时出发向C和B运动(任何一个点到达即停止),在运动过程中,则线段CP的最小值为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,OP为一墙面,它与地面OQ垂直,有一根木棒AB如图放置,点C是它的中点,现在将木棒的A点在OP上由A点向下滑动,点B由O点向OQ方向滑动,直到AB横放在地面为止.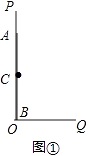
(1)在AB滑动过程中,点C经过的路径可以用下列哪个图象来描述( )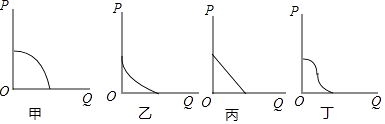
(2)若木棒长度为2m,如图②射线OM与地面夹角∠MOQ=60°,当AB滑动过程中,与OM并于点D,分别求出当AD= ![]() 、AD=1、AD=
、AD=1、AD= ![]() 时,OD的值.
时,OD的值.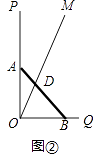
(3)如图③,是一个城市下水道,下水道入口宽40cm,下水道水平段高度为40cm,现在要想把整根木棒AB通入下水道水平段进行工作,那么这根木棒最长可以是(cm)(直接写出结果,结果四舍五入取整数).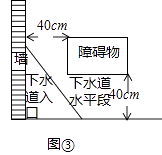
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将长方形ABCD沿着对角线BD折叠,使点C落在![]() 处,
处,![]() 交AD于点E.
交AD于点E.
(1)试判断△BDE的形状,并说明理由;
(2)若![]() ,
,![]() ,求△BDE的面积.
,求△BDE的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
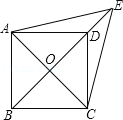
【题目】如图,已知平行四边形ABCD中,对角线AC,BD交于点O,E是BD延长线上的点,且△ACE是等边三角形.
(1)求证:四边形ABCD是菱形;
(2)若∠AED=2∠EAD,求证:四边形ABCD是正方形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们规定:![]() =
=![]() (a≠0),即a的负P次幂等于a的p次幂的倒数.例:
(a≠0),即a的负P次幂等于a的p次幂的倒数.例:![]() =
=![]()
(1)计算:![]() =__;
=__;![]() =__;
=__;
(2)如果![]() =
=![]() ,那么p=__;如果
,那么p=__;如果![]() =
=![]() ,那么a=__;
,那么a=__;
(3)如果![]() =
=![]() ,且a、p为整数,求满足条件的a、p的取值.
,且a、p为整数,求满足条件的a、p的取值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2016新疆)如图,ABCD中,AB=2,AD=1,∠ADC=60°,将ABCD沿过点A的直线l折叠,使点D落到AB边上的点D′处,折痕交CD边于点E.
(1)求证:四边形BCED′是菱形;
(2)若点P时直线l上的一个动点,请计算PD′+PB的最小值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“中华人民共和国道路交通管理条例”规定:小汽车在城市街道上行驶速度不得超过70 km/h.如图,一辆小汽车在一条城市街路上直道行驶,某一时刻刚好行驶到路对面车速检测仪正前方30 m处,过了2 s后,测得小汽车与车速检测仪间距离为50 m,这辆小汽车超速了吗?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com