
 ��ͼ��ƽ��ֱ������ϵ�У�ֱ��AB��x�ᣬy��ֱ���A��3��0����B��0��$\sqrt{3}$�����㣬��C��D�ֱ�Ϊ�߶�AB��OA�ϵ�һ���㣮
��ͼ��ƽ��ֱ������ϵ�У�ֱ��AB��x�ᣬy��ֱ���A��3��0����B��0��$\sqrt{3}$�����㣬��C��D�ֱ�Ϊ�߶�AB��OA�ϵ�һ���㣮���� ��1�����ݡ�ƽ���߷��߶γɱ�������֪CD��OB��
��2�������������ε����֮�ȵ������Ʊȵ�ƽ���õ�AD�ij��ȣ��������D�����ꣻ
��3����Ϊ��AOB=90�㣬������P��O��BΪ��������������OBA����������̽�֣�
����OBP=90��ʱ����ͼ
������BOP�ס�OBA�����BOP=��BAO=30�㣬BP=$\sqrt{3}$OB=3��P1��3��$\frac{\sqrt{3}}{3}$����
������BPO�ס�OBA�����BPO=��BAO=30�㣬OP=$\frac{\sqrt{3}}{3}$OB=1��P2��1��$\sqrt{3}$����
�۹���P��OP��BC�ڵ�P����ʱ��PBO�ס�OBA����BOP=��BAO=30�㣬OP=$\sqrt{3}$BP������P��PM��OA�ڵ�M����OPM=30�㣬OM=$\frac{1}{2}$OP��PM=$\sqrt{3}$OM���Ӷ����P�����꣮
������POB�ס�OBA�����OBP=��BAO=30�㣬��POM=30�㣬����PM=$\frac{\sqrt{3}}{3}$OM��P4��$\frac{3}{4}$��$\frac{\sqrt{3}}{4}$��������POB=90��ʱ����P��x���ϣ�������Ҫ��
��� �⣺��1��CD��OBƽ�У��������£�
��A��3��0����B��0��$\sqrt{3}$����
��OA=3��OB=$\sqrt{3}$��
��AB=$\sqrt{O{A}^{2}+O{B}^{2}}$=2$\sqrt{3}$��
��AC=$\sqrt{3}$��AD=$\frac{3}{2}$��
��$\frac{AD}{AO}$=$\frac{AC}{AB}$=$\frac{1}{2}$��
��CD��OB��
��2����S��OAB=$\frac{1}{2}$OA•OB=$\frac{1}{2}$��3��$\sqrt{3}$=$\frac{3\sqrt{3}}{2}$��S�ı���OBCD=$\sqrt{3}$��
��S��ACD=S��OAB-S�ı���OBCD=$\frac{\sqrt{3}}{2}$��
�ߡ�ACD�ס�ABO��
��$\frac{AD}{OA}$=$\sqrt{\frac{{S}_{��ACD}}{{S}_{��ABO}}}$=$\sqrt{\frac{\frac{\sqrt{3}}{2}}{\frac{3\sqrt{3}}{2}}}$=$\frac{\sqrt{3}}{3}$����AD=$\frac{\sqrt{3}}{3}$��3=$\sqrt{3}$��
��AD=3-$\sqrt{3}$��
��D��3-$\sqrt{3}$��0����
��3������OBP=90��ʱ����ͼ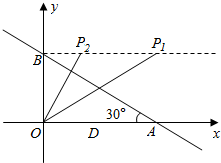
������BOP�ס�BAO��
���BOP=��BAO=30�㣬BP=$\sqrt{3}$OB=3��
��P1��3��$\sqrt{3}$����
������BPO�ס�BAO��
���BPO=��BAO=30�㣬BP=$\frac{\sqrt{3}}{3}$OB=1��
��P2��1��$\sqrt{3}$����
����OPB=90��ʱ
�۹���P��OP��BA�ڵ�P����ͼ����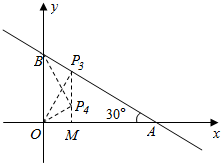
��ʱ��PBO�ס�OBA����BOP=��BAO=30��
����P��PM��OA�ڵ�M��
��Rt��PBO��BP=$\frac{1}{2}$OB=$\frac{\sqrt{3}}{2}$��
OP=$\sqrt{3}$BP=$\frac{3}{2}$��
����Rt��PMO�У���OPM=30�㣬
��OM=$\frac{1}{2}$OP=$\frac{3}{4}$��PM=$\sqrt{3}$OM=$\frac{3\sqrt{3}}{4}$��
��P3��$\frac{3}{4}$��$\frac{3\sqrt{3}}{4}$����
������POB�ס�OBA����ͼ����
���OBP=��BAO=30�㣬��POM=30�㣮
��PM=$\frac{\sqrt{3}}{3}$OM=$\frac{\sqrt{3}}{4}$��
��P4��$\frac{3}{4}$��$\frac{\sqrt{3}}{4}$�����ɶԳ���Ҳ�ɵõ���P4�����꣩��
����POB=90��ʱ����P��x���ϣ�������Ҫ��
�ۺϵã����������ĵ����ĸ����ֱ��ǣ�P1��3��$\sqrt{3}$����P2��1��$\sqrt{3}$����P3��$\frac{3}{4}$��$\frac{3\sqrt{3}}{4}$����P4��$\frac{3}{4}$��$\frac{\sqrt{3}}{4}$����
���� �����ۺϿ������ô���ϵ������һ�κ����Ľ���ʽ�����������ε��й�֪ʶ������������ⳣ�õ��������ۡ����ν�ϡ����̺�ת������ѧ˼�뷽����


 �������Ͽ�ʱͬ��ѵ��ϵ�д�
�������Ͽ�ʱͬ��ѵ��ϵ�д� �������ͬ����ϰϵ�д�
�������ͬ����ϰϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��ͼ��ʾ����һ��ƽ��ȥ��һ��Բ���壬�������״�����ǣ�������
��ͼ��ʾ����һ��ƽ��ȥ��һ��Բ���壬�������״�����ǣ�������| A�� |  | B�� |  | C�� |  | D�� |  |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ��?ABCD�У��Խ���AC��BD�ཻ�ڵ�O����ABC�ǵȱ������Σ�AB=6cm��
��ͼ��?ABCD�У��Խ���AC��BD�ཻ�ڵ�O����ABC�ǵȱ������Σ�AB=6cm���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
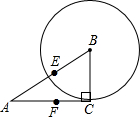 ��ͼ����ֱ��������ABC�У���C=90�㣬AC=4��BC=3��E��F�ֱ�ΪAB��AC���е㣬��BΪԲ�ģ�BCΪ�뾶��Բ�����жϵ�A��C��E��F���B��λ�ù�ϵ����˵�����ɣ�
��ͼ����ֱ��������ABC�У���C=90�㣬AC=4��BC=3��E��F�ֱ�ΪAB��AC���е㣬��BΪԲ�ģ�BCΪ�뾶��Բ�����жϵ�A��C��E��F���B��λ�ù�ϵ����˵�����ɣ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
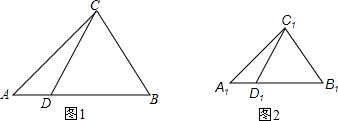
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com