
 ��ͼ��ֱ��y=kx+4�뺯��y=$\frac{m}{x}$��x��0��m��0����ͼ����A��B���㣬����x��y��ֱ���C��D���㣮
��ͼ��ֱ��y=kx+4�뺯��y=$\frac{m}{x}$��x��0��m��0����ͼ����A��B���㣬����x��y��ֱ���C��D���㣮���� ��1��������ֱ��ƽ�еõ�k=-1����ȷ��C��0��4������A��t��-t��+4�������������������ʽ��$\frac{1}{2}$��4��t=2�����t=1���Ӷ��õ�A�����꣬Ȼ�����÷���������ͼ���ϵ����������ȷ��m��ֵ��
��2������A��x1��y1����B��x2��y2��������x1��x2��y1��y2��������S��COD=$\sqrt{2}$S��AOB����S��COD=$\sqrt{2}$��S��BOD-S��BOC�������������������ʽ�õ�$\frac{1}{2}$•OC•OD=$\sqrt{2}$�� $\frac{1}{2}$•OC•y1-$\frac{1}{2}$•OC•y2����������OD=$\sqrt{2}$��y1-y2������AH��OD=1��$\sqrt{2}$��
������OD=4����y1-y2��2=8��������ȫƽ����ʽ���εõ���y1+y2��2-4y1y2=8��������y=$\frac{m}{x}$�ɵ�x=$\frac{m}{y}$������y=kx+4��y2-4y-km=0�����ݸ���ϵ���Ĺ�ϵ��y1+y2=4��y1•y2=-km������16+4km=8�����ǵõ�k=-$\frac{2}{m}$��
��3����B��x��Ĵ��ߣ�����ֱ�ΪN����ͼ�����õȽǵ������ȵá�EAP=��BPN������ж�Rt��EAP��Rt��NPB���������Ʊȵ�$\frac{{y}_{1}}{{x}_{2}-2}$=$\frac{2-{x}_{1}}{{y}_{2}}$�����εã�x1-2����x2-2��+y1y2=0������x=$\frac{m}{y}$�ã�$\frac{m}{{y}_{1}}$-2����$\frac{m}{{y}_{2}}$-2��+y1y2=0������m2-2m��y1+y2��+4y1y2+��y1y2��2=0�����Ű�y1+y2=4��y1•y2=2����ɵ�m2-8m+12=0�����m=2��6��Ȼ������Ӧ��k��ֵ��
��� �⣺��1����ֱ��y=kx+4��ֱ��y=-x-2ƽ�У�
��k=-1��
��һ�κ�������ʽΪy=-x-4��
��x=0ʱ��y=-x+4=4����C��0��4����
��A��t��-t��+4����
�ߡ�AOD���Ϊ2��
��$\frac{1}{2}$��4��t=2�����t=1��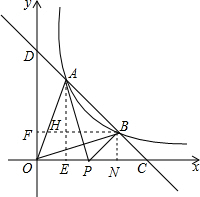
��A��1��3����
��m=1��3=3��
��2������A��x1��y1����B��x2��y2��������x1��x2��y1��y2����
��S��COD=$\sqrt{2}$S��AOB��
��S��COD=$\sqrt{2}$��S��AOC-S��BOC��
��$\frac{1}{2}$•OC•OD=$\sqrt{2}$�� $\frac{1}{2}$•OC•y1-$\frac{1}{2}$•OC•y2����
��OD=$\sqrt{2}$��y1-y2����
��AH=y1-y2��
��AH��OD=$\frac{\sqrt{2}}{2}$
�ڡ�OD=4��
�ࣨy1-y2��2=8������y1+y2��2-4y1y2=8��
��y=$\frac{m}{x}$�ɵ�x=$\frac{m}{y}$������y=kx+4��y2-4y-km=0��
��y1+y2=4��y1•y2=-km��
��16+4km=8����k=-$\frac{2}{m}$��
��m��k�Ĺ�ϵʽΪk=-$\frac{2}{m}$��m��0����
��3������k��mʹ�á�APBΪֱ�������Σ��ҡ�APB=90�㣮
��B��x��Ĵ��ߣ�����ֱ�ΪN����ͼ��
����APB=90�㣬���APE+��BPN=90�㣬
�ߡ�APE+��PAE=90�㣬
���EAP=��BPN��
��Rt��EAP��Rt��NPB��
��$\frac{AE}{PN}$=$\frac{PE}{BN}$����$\frac{{y}_{1}}{{x}_{2}-2}$=$\frac{2-{x}_{1}}{{y}_{2}}$��
�ࣨx1-2����x2-2��+y1y2=0��
�ࣨ$\frac{m}{{y}_{1}}$-2����$\frac{m}{{y}_{2}}$-2��+y1y2=0��
��m2-2m��y1+y2��+4y1y2+��y1y2��2=0��
��y1+y2=4��y1•y2=2��
��m2-8m+12=0�����m=2��6��
��m=2��k=-$\frac{2}{m}$=-1����m=6��k=-$\frac{2}{m}$=-$\frac{1}{3}$��
�����k��mʹ�á�APBΪֱ�������Σ��ҡ�APB=90�㣮
���� ���⿼���˷����������ۺ��⣺�������շ���������ͼ���ϵ������������һ�κ���ͼ���ϵ������������������������һ�κ����Ľ������꣬������ø���ϵ���Ĺ�ϵ�����������Ʊȼ����߶εij���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
| +0.030 | -0.018 | +0.026 | -0.025 | +0.015 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
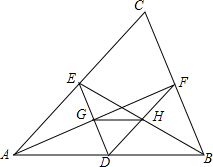 ��ͼ��ʾ��DΪ��ABC�ı�AB�ϵĵ㣬��D����DE��BC��DF��AC��AF��DE�ڵ�G��BE��DF�ڵ�H����֤��GH��AB��
��ͼ��ʾ��DΪ��ABC�ı�AB�ϵĵ㣬��D����DE��BC��DF��AC��AF��DE�ڵ�G��BE��DF�ڵ�H����֤��GH��AB���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
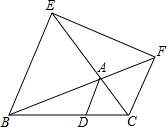 ��ͼ���ӡ�ABC��������ƽ����AD��EB��FC��������Ա����ӳ����ཻ��D��E��F����֤��S��DEF=2S��ABC��
��ͼ���ӡ�ABC��������ƽ����AD��EB��FC��������Ա����ӳ����ཻ��D��E��F����֤��S��DEF=2S��ABC���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��֪ƽ�����ĵ�A��B��C��D����ͼ��
��֪ƽ�����ĵ�A��B��C��D����ͼ���鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com