
【题目】在![]() 中,
中,![]() 垂足为
垂足为![]() ,点
,点![]() 在
在![]() 上,
上,![]() 连接
连接![]() 并延长交
并延长交![]() 于点
于点![]() ,连接
,连接![]() .
.
![]() 求证:
求证:![]()
![]() 求证:
求证:![]()
【答案】(1)详见解析;(2)详见解析.
【解析】
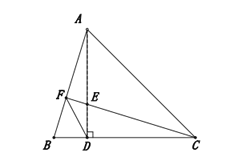
(1)根据三角形高线的定义求出∠ADB=∠CDE=90°,并判断出△ACD是等腰直角三角形,根据等腰直角三角形的性质可得AD=CD,然后利用“边角边”证明△ABD和△CED全等,根据全等三角形对应角相等可得结论;
(2)在EC上截取EG=BF,根据全等三角形对应角相等可得∠B=∠CED,然后利用“边角边”证明△BDF和△EDG全等,根据全等三角形对应边相等可得DF=DG,全等三角形对应角相等可得∠BDF=∠EDG,再求出∠FDG=90°,判断出△DFG是等腰直角三角形,即可得到结论.
(1)∵AD是△ABC的高,∠ACB=45°,∴∠ADB=∠CDE=90°,△ACD是等腰直角三角形,∴AD=CD.
在△ABD和△CED中,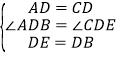 ,∴△ABD≌△CED(SAS),∴∠BAD=∠ECD;
,∴△ABD≌△CED(SAS),∴∠BAD=∠ECD;
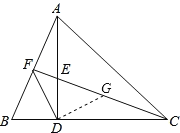
(2)如图,在EC上截取EG=BF.
∵△ABD≌△CED,∴∠B=∠CED.在△BDF和△EDG中,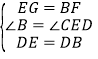 ,∴△BDF≌△EDG(SAS),∴DF=DG,∠BDF=∠EDG,∴∠FDG=∠FDE+∠EDG=∠FDE+∠BDF=∠ADB=90°,∴△DFG是等腰直角三角形,∴∠DFE=45°.
,∴△BDF≌△EDG(SAS),∴DF=DG,∠BDF=∠EDG,∴∠FDG=∠FDE+∠EDG=∠FDE+∠BDF=∠ADB=90°,∴△DFG是等腰直角三角形,∴∠DFE=45°.


 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AD是BC边上的中线,AE是BC边上的高.
(1)若∠ACB=100°,求∠CAE的度数;
(2)若S△ABC=12,CD=4,求高AE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某种动物的身高y(dm)是其腿长x(dm)的一次函数.当动物的腿长为6dm时,身高为45.5dm;当动物的腿长为14dm时,身高为105.5dm.
(1)写出y与x之间的关系式;
(2)当该动物腿长10dm时,其身高为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC三个顶点的坐标分别为A(1,1),B(4,2),C(3,4),
(1)画出△ABC关于y轴的对称图形△A1B1C1,并写出点B1的坐标;
(2)在x轴上求作一点P,使△PAB的周长最小,并直接写出点P的坐标.
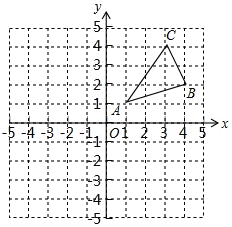
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校园文学社为了解本校学生对本社一种报纸四个版面的喜欢情况,随机抽取部分学生做了一次问卷调查,要求学生选出自己喜欢的一个版面,将调查数据进行了整理、绘制成部分统计图如下:

请根据图中信息,解答下列问题:
(1)第一版=____%,“第四版”对应扇形的圆心角为________°;
(2)请你补全条形统计图;
(3)若该校有1200名学生,请你估计全校学生中最喜欢“第三版”的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学为了绿化校园,计划购买一批榕树和香樟树,经市场调查,榕树的单价比香樟树少20元,购买3棵榕树和2棵香樟树共需340元.
(1)榕树和香樟树的单价各是多少?
(2)根据学校实际情况,需购买两种树苗共150棵,总费用不超过10840元,且购买香樟树的棵数不少于榕树的1.5倍,请你算算该校本次购买榕树和香樟树共有哪几种方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】三角形ABC(记作△ABC)在8×8方格中,位置如图所示,A(-3,1),B(-2,4).

(1)请你在方格中建立直角坐标系,并写出C点的坐标;
(2)把△ABC向下平移1个单位长度,再向右平移2个单位长度,请你画出平移后的△A1B1C1,若△ABC内部一点P的坐标为(a,b),则点P的对应点P1的坐标是 .
(3)在x轴上存在一点D,使△DB1C1的面积等于3,求满足条件的点D的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com