
【题目】已知△ABC中, ![]() ,
, ![]() ,△CDE中,
,△CDE中, ![]() ,CD=DE=5,
,CD=DE=5,
连接接BE,取BE中点F,连接AF、DF.
(1)如图1,若![]() 三点共线,
三点共线, ![]() 为
为![]() 中点.
中点.
①直接指出![]() 与
与![]() 的关系______________;
的关系______________;
②直接指出![]() 的长度______________;
的长度______________;
(2)将图(1)中的△CDE绕![]() 点逆时针旋转
点逆时针旋转![]() (如图2,
(如图2, ![]() ),试确定
),试确定![]() 与
与![]() 的关系,并说明理由;
的关系,并说明理由;
(3)在(2)中,若![]() ,请直接指出点
,请直接指出点![]() 所经历的路径长.
所经历的路径长.


图1 图2
【答案】(1)①![]() ,
, ![]() ,②
,②![]() ;(2)
;(2)![]() ,
, ![]() ,理由见解析;(3)
,理由见解析;(3)![]() 或
或![]()
【解析】试题分析:(1)①如图,过点F M⊥CD于M,FN⊥AC交CA的延长线于点N,根据已知条件易证四边形FMCN为正方形,可得FN=FM,再证△FNA≌△FMD,即可得∠NFA=∠DFM,DF=AF,所以∠NFA+∠AFM=∠DFM+∠AFM=∠DFA=90°,即可证得![]() ;②根据勾股定理求得BC=
;②根据勾股定理求得BC=![]() ,EC=5
,EC=5![]() ,因
,因![]() 为
为![]() 中点,F为BE的中点,可得CH=BH=
中点,F为BE的中点,可得CH=BH=![]() ,EB=5
,EB=5![]() -
-![]() =
=![]() ,EF=BF=
,EF=BF=![]() ,所以FH=BF+BH=
,所以FH=BF+BH=![]() ;
;
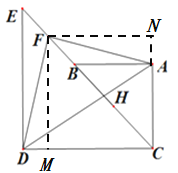
(2) ![]() ,
, ![]() ,延长
,延长![]() 至
至![]() 使
使![]() ,连接
,连接![]() ,延长
,延长![]() 交
交![]() 于
于![]() ,
, ![]() ,
, ![]() ,
, ![]() ,再证得
,再证得![]() ,由
,由![]() ,CD=DE,根据SAS判定
,CD=DE,根据SAS判定![]() ,
, ![]() ,
, ![]() ,
, ![]() ,根据等腰直角三角形的性质可得
,根据等腰直角三角形的性质可得![]() ,
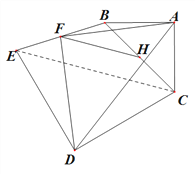
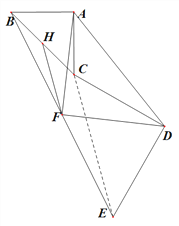
, ![]() ; (3)如图,当旋转
; (3)如图,当旋转![]() 或
或![]() 时,
时, ![]() ,AD=7,点
,AD=7,点![]() 经历的路径长为
经历的路径长为![]() 或
或![]() .
.
试题解析:
(1)(1)①![]() ,
, ![]()
②![]()
(2)结论: ![]() ,
, ![]() 理由如下:
理由如下:
延长![]() 至
至![]() 使
使![]() ,连接
,连接![]() ,延长
,延长![]() 交
交![]() 于
于![]()
![]() ,
, ![]() ,
, ![]() ,
, ![]()
![]() ,
, ![]()
![]() ,
, ![]() ,
, ![]()
![]() ,
, ![]() ,
, ![]() ,
, ![]()
![]() ,
, ![]()
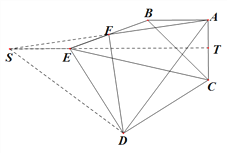
(3)旋转![]() 或
或![]() 时,
时, ![]() ,AD=7,点
,AD=7,点![]() 经历的路径长为
经历的路径长为![]() 或
或![]()


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线![]() 与坐标轴分别交于点A、点B、点C,并且∠ACB=90,AB=10.
与坐标轴分别交于点A、点B、点C,并且∠ACB=90,AB=10.
(1)求证:△OAC∽△OCB;
(2)求该抛物线的解析式;
(3)若点P是(2)中抛物线对称轴上的一个动点,是否存在点P使得△PAC为等腰三角形,若存在,请直接写出点P的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在平面直角坐标系xOy中,O为坐标原点,线段AB的两个端点A(0,2),B(1,0)分别在y轴和x轴的正半轴上,点C为线段AB的中点,现将线段BA绕点B按顺时针方向旋转90°得到线段BD,抛物线y=ax2+bx+c(a≠0)经过点D.
(1)如图1,若该抛物线经过原点O,且a=﹣![]() .
.
①求点D的坐标及该抛物线的解析式;
②连结CD,问:在抛物线上是否存在点P,使得∠POB与∠BCD互余?若存在,请求出所有满足条件的点P的坐标,若不存在,请说明理由;
(2)如图2,若该抛物线y=ax2+bx+c(a≠0)经过点E(1,1),点Q在抛物线上,且满足∠QOB与∠BCD互余.若符合条件的Q点的个数是3个,请直接写出a的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】北京第一条地铁线路于1971年1月15日正式开通运营.截至2017年1月,北京地铁共有19条运营线路,覆盖北京市11个辖区.据统计,2017 年地铁每小时客运量是2002年地铁每小时客运量的4倍,2017年客运240万人所用的时间比2002年客运240万人所用的时间少30小时,求2017年地铁每小时的客运量?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】三张形状、大小相同但画面不同的风景图片,都按同样的方式剪成相同的三段,然后将上、中、下三段分别混合洗匀,从三堆图片中随机各抽出一张, 求这三张图片恰好组成一张完整风景图片的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在□ABCD中,对角线AC、BD相交于点O,AB⊥AC,AB=3cm,BC=5cm.点P从A点出发沿AD方向匀速运动,速度为1cm/s.连结PO并延长交BC于点Q,设运动时间为t(0<t<5).
(1)当t为何值时,四边形ABQP是平行四边形?
(2)设四边形OQCD的面积为y(cm2),求y与t之间的函数关系式;
(3)是否存在某一时刻t,使点O在线段AP的垂直平分线上?若存在,求出t的值;若不存在,请说明理由.

 备用图
备用图
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小红星期天从家里出发骑车去舅舅家做客,当她骑了一段路时,想起要买个礼物送给表弟,于是又折回到刚经过的一家商店,买好礼物后又继续骑车去舅舅家,以下是她本次去舅舅家所用的时间与路程的关系式示意图.根据图中提供的信息回答下列问题:
(1)小红家到舅舅家的路程是______米,小红在商店停留了______分钟;
(2)在整个去舅舅家的途中哪个时间段小红骑车速度最快,最快的速度是多少米/分
(3)本次去舅舅家的行程中,小红一共行驶了多少米?一共用了多少分钟?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点E在△ABC的边AB上,∠C=90°,∠BAC的平分线交BC于点D,且D在以AE为直径的⊙O上.
(1)求证:BC是⊙O的切线;
(2)已知∠B=30°,CD=4,求线段AB的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD的一边BC与⊙O相切于G,DC=6,且对角线BD经过圆心O,AD交⊙O于点E,连接BE,BE恰好是⊙O的切线,已知点P在对角线BD上运动,若以B、P、G三点构成的三角形与△BED相似,则BP=______.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com