
【题目】如图1,反比例函数![]() (x>0)的图象经过点A(
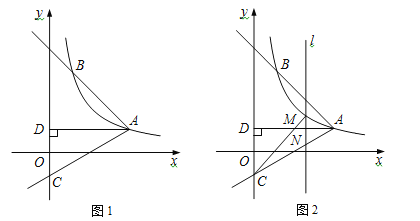
(x>0)的图象经过点A(![]() ,1),射线AB与反比例函数图象交于另一点B(1,a),射线AC与y轴交于点C,∠BAC=75°,AD⊥y轴,垂足为D.
,1),射线AB与反比例函数图象交于另一点B(1,a),射线AC与y轴交于点C,∠BAC=75°,AD⊥y轴,垂足为D.
(1)求k的值;
(2)求tan∠DAC的值及直线AC的解析式;
(3)如图2,M是线段AC上方反比例函数图象上一动点,过M作直线l⊥x轴,与AC相交于点N,连接CM,求△CMN面积的最大值.
【答案】(1)![]() ;(2)
;(2)![]() ,
,![]() ;(3)
;(3)![]()
【解析】试题分析:(1)根据反比例函数图象上点的坐标特征易得k=2![]() ;
;
(2)作BH⊥AD于H,如图1,根据反比例函数图象上点的坐标特征确定B点坐标为(1,2![]() ),则AH=2
),则AH=2![]() ﹣1,BH=2
﹣1,BH=2![]() ﹣1,可判断△ABH为等腰直角三角形,所以∠BAH=45°,得到∠DAC=∠BAC﹣∠BAH=30°,根据特殊角的三角函数值得tan∠DAC=
﹣1,可判断△ABH为等腰直角三角形,所以∠BAH=45°,得到∠DAC=∠BAC﹣∠BAH=30°,根据特殊角的三角函数值得tan∠DAC=![]() ;由于AD⊥y轴,则OD=1,AD=2
;由于AD⊥y轴,则OD=1,AD=2![]() ,然后在Rt△OAD中利用正切的定义可计算出CD=2,易得C点坐标为(0,﹣1),于是可根据待定系数法求出直线AC的解析式为y=
,然后在Rt△OAD中利用正切的定义可计算出CD=2,易得C点坐标为(0,﹣1),于是可根据待定系数法求出直线AC的解析式为y=![]() x﹣1;
x﹣1;
(3)利用M点在反比例函数图象上,可设M点坐标为(t,![]() )(0<t<2
)(0<t<2![]() ),由于直线l⊥x轴,与AC相交于点N,得到N点的横坐标为t,利用一次函数图象上点的坐标特征得到N点坐标为(t,
),由于直线l⊥x轴,与AC相交于点N,得到N点的横坐标为t,利用一次函数图象上点的坐标特征得到N点坐标为(t,![]() t﹣1),则MN=
t﹣1),则MN=![]() ﹣
﹣![]() t+1,根据三角形面积公式得到S△CMN=
t+1,根据三角形面积公式得到S△CMN=![]() t(
t(![]() ﹣
﹣![]() t+1),再进行配方得到S=﹣
t+1),再进行配方得到S=﹣![]() (t﹣
(t﹣![]() )2+
)2+![]() (0<t<2
(0<t<2![]() ),最后根据二次函数的最值问题求解.
),最后根据二次函数的最值问题求解.
试题解析:(1)把A(2![]() ,1)代入y=
,1)代入y=![]() ,得k=2
,得k=2![]() ×1=2
×1=2![]() ;
;
(2)作BH⊥AD于H,如图1,
把B(1,a)代入反比例函数解析式y=![]() ,得a=2
,得a=2![]() ,
,
∴B点坐标为(1,2![]() ),
),
∴AH=2![]() ﹣1,BH=2
﹣1,BH=2![]() ﹣1,
﹣1,
∴△ABH为等腰直角三角形,∴∠BAH=45°,
∵∠BAC=75°,∴∠DAC=∠BAC﹣∠BAH=30°,
∴tan∠DAC=tan30°=![]() ;
;
∵AD⊥y轴,∴OD=1,AD=2![]() ,∵tan∠DAC=
,∵tan∠DAC=![]() =
=![]() ,
,
∴CD=2,∴OC=1,
∴C点坐标为(0,﹣1),
设直线AC的解析式为y=kx+b,
把A(2![]() ,1)、C(0,﹣1)代入得
,1)、C(0,﹣1)代入得![]() ,解得
,解得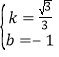 ,
,
∴直线AC的解析式为y=![]() x﹣1;
x﹣1;
(3)设M点坐标为(t,![]() )(0<t<2
)(0<t<2![]() ),
),
∵直线l⊥x轴,与AC相交于点N,∴N点的横坐标为t,∴N点坐标为(t,![]() t﹣1),
t﹣1),
∴MN=![]() ﹣(
﹣(![]() t﹣1)=
t﹣1)=![]() ﹣
﹣![]() t+1,
t+1,
∴S△CMN=![]() t(
t(![]() ﹣
﹣![]() t+1)=﹣
t+1)=﹣![]() t2+
t2+![]() t+
t+![]() =﹣
=﹣![]() (t﹣
(t﹣![]() )2+
)2+![]() (0<t<2
(0<t<2![]() ),
),
∵a=﹣![]() <0,∴当t=
<0,∴当t=![]() 时,S有最大值,最大值为
时,S有最大值,最大值为![]() .
.


 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,∠BAD的平分线交BC于点E,∠ABC的平分线交AD于点F.若BF=12,AB=10,则AE的长为( )

A. 10 B. 12 C. 16 D. 18
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中考体育测试前,某区教育局为了了解选报引体向上的初三男生的成绩情况,随机抽测了本区部分选报引体向上项目的初三男生的成绩,并将测试得到的成绩绘成了下面两幅不完整的统计图:
请你根据图中的信息,解答下列问题:
(![]() )写出扇形图中
)写出扇形图中![]() __________
__________![]() ,并补全条形图.
,并补全条形图.
(![]() )在这次抽测中,测试成绩的众数和中位数分别是__________个、__________个.
)在这次抽测中,测试成绩的众数和中位数分别是__________个、__________个.
(![]() )该区体育中考选报引体向上的男生共有
)该区体育中考选报引体向上的男生共有![]() 人,如果体育中考引体向上达
人,如果体育中考引体向上达![]() 个以上(含
个以上(含![]() 个)得满分,请你估计该区体育中考中选报引体向上的男生能获得满分的有多少名?
个)得满分,请你估计该区体育中考中选报引体向上的男生能获得满分的有多少名?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】依据下列解方程![]() 的过程,请在前面括号内填写变形步骤,在后面的括号内填写变形依据.
的过程,请在前面括号内填写变形步骤,在后面的括号内填写变形依据.
解:原方程可变形为![]() ,
,
去分母,得![]() .(____________________)
.(____________________)
去括号,得![]() .(____________________)
.(____________________)
移项,得![]() .(____________________)
.(____________________)
合并,得![]() .(合并同类项)
.(合并同类项)
(______),得![]() .(______________)
.(______________)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料:
![]() ,
,![]() ,
,![]() ,
,
由以上三个等式相加,可得
![]()
![]() .
.
读完以上材料,请你计算下列各题:
(1)![]() (写出过程);
(写出过程);
(2)![]() __________________________(直接写出答案);
__________________________(直接写出答案);
(3)![]() _____________________(直接写出答案).
_____________________(直接写出答案).
查看答案和解析>>
科目:初中数学 来源: 题型:
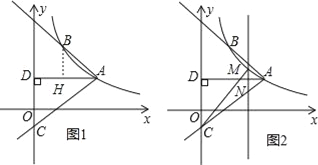
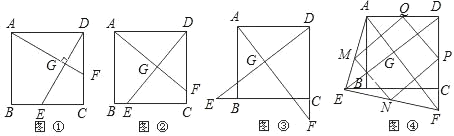
【题目】如图1,在正方形ABCD中,点E、F分别为边BC、CD的中点,AF、DE相交于点G,则可得结论:①AF=DE,②AF⊥DE(不须证明).
(1)如图②,若点E、F不是正方形ABCD的边BC、CD的中点,但满足CE=DF,则上面的结论①、②是否仍然成立;(请直接回答“成立”或“不成立”)
(2)如图③,若点E、F分别在正方形ABCD的边CB的延长线和DC的延长线上,且CE=DF,此时上面的结论①、②是否仍然成立?若成立,请写出证明过程;若不成立,请说明理由.
(3)如图④,在(2)的基础上,连接AE和EF,若点M、N、P、Q分别为AE、EF、FD、AD的中点,请先判断四边形MNPQ是“矩形、菱形、正方形、等腰梯形”中的哪一种,并写出证明过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2014年1月,国家发改委出台指导意见,要求2015年底前,所有城市原则上全面实行居民阶梯水价制度.小明为了解市政府调整水价方案的社会反响,随机访问了自己居住在小区的部分居民,就“每月每户的用水量”和“调价对用水行为改变”两个问题进行调查,并把调查结果整理成下面的图1,图2.

小明发现每月每户的用水量在5m2-35m2之间,有8户居民对用水价格调价涨幅抱无所谓,不用考虑用水方式的改变.根据小明绘制的图表和发现的信息,完成下列问题:
(1)n= ,小明调查了 户居民,并补全图1;
(2)每月每户用水量的中位数和众数分别落在什么范围?
(3)如果小明所在的小区有1800户居民,请你估计“视调价涨幅采取相应的用水方式改变”的居民户数有多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】给出以下命题:
①函数![]() 是偶函数,但不是奇函数;
是偶函数,但不是奇函数;
②已知回归直线方程为![]() ,样本点的中心为
,样本点的中心为![]() ,则
,则![]() ;
;
③函数![]() 图象关于点
图象关于点![]() 对称且在
对称且在![]() 上单调递增;
上单调递增;
④根据党中央关于“精准”脱贫的要求,我州某农业经济部门决定派出五位相关专家对三个贫困地区进行调研,每个地区至少派遣一位专家,其中甲、乙两位专家需要派遣至同一地区,则不同的派遣方案种数有![]() 种;
种;
⑤已知双曲线![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,过
,过![]() 的直线交双曲线右支于
的直线交双曲线右支于![]() 两点,且
两点,且![]() ,若
,若![]() ,则双曲线的离心率为
,则双曲线的离心率为![]() .
.
其中正确的命题序号为_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com