
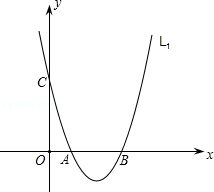
��ͼ����֪���κ���L1��y=x2��4x+3��x�ύ��A��B���㣨��A�ڵ�B��ߣ�����y�ύ�ڵ�C��
��1��д�����κ���L1�Ŀ��ڷ��Գ���Ͷ������ꣻ
��2���о����κ���L2��y=kx2��4kx+3k��k��0����
��д�����κ���L2����κ���L1�й�ͼ���������ͬ�����ʣ�
����ֱ��y=8k��������L2����E��F���㣬���߶�EF�ij����Ƿ����仯��������ᣬ�����EF�ij��ȣ�����ᣬ��˵�����ɣ�
���㣺���κ����ۺ��⡣
ר�⣺�ۺ��⡣
��������1��������y=ax2+bx+c�У�a��ֵ�����������ߵĿ��ڷ���a��0ʱ�������ߵĿ������ϣ�a��0ʱ�������ߵĿ������£�
�����ߵĶԳ��᷽�̣�x=��![]() ���������꣺����
���������꣺����![]() ��
��![]() ����
����
��2�����º�������ԭ�����ĸ���ϵ��ͬʱ����k���ã���˴Ӷ��κ�����ͼ�������ʽ��ϵ���Ĺ�ϵ���ֽ��з�����
����ϵֱ�ߺ�������L2�Ľ���ʽ���������E��F�����꣬�����ɱ�ʾ��EF�ij������ó���Ϊ��ֵ�����߶�EF�ij����ᷢ���仯��
��𣺽⣺��1��������y=x2��4x+3�У�a=1��b=��4��c=3��
�ੁ![]() =��
=��![]() =2��
=2��![]() =
=![]() =��1��
=��1��
����κ���L1�Ŀ������ϣ��Գ�����ֱ��x=2���������꣨2����1����
��2���ٶ��κ���L2��L1�й�ͼ���������ͬ�����ʣ�
�Գ���Ϊx=2��ĺ�����Ϊ2��
������A��1��0����B��3��0�����㣻
���߶�EF�ij��Ȳ��ᷢ���仯��
��ֱ��y=8k��������L2����E��F���㣬
��kx2��4kx+3k=8k��
��k��0����x2��4x+3=8��
��ã�x1=��1��x2=5����EF=x2��x1=6��
���߶�EF�ij��Ȳ��ᷢ���仯��

![]() ������������Ҫ������Ǻ����Ļ���֪ʶ���У����κ��������ʡ�����ͼ������Ľⷨ�ȣ��ѶȲ�����Ҫ�������գ�
������������Ҫ������Ǻ����Ļ���֪ʶ���У����κ��������ʡ�����ͼ������Ľⷨ�ȣ��ѶȲ�����Ҫ�������գ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
| 5 |
| 2 |
| 13 |
| 4 |
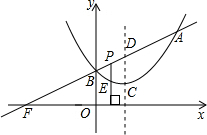 ���������BOF���ƣ������ڣ������P������ꣻ�������ڣ���˵�����ɣ�
���������BOF���ƣ������ڣ������P������ꣻ�������ڣ���˵�����ɣ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
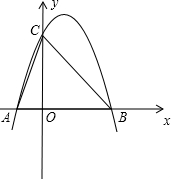
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
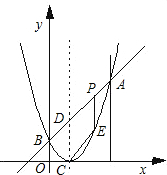 ��ͼ����֪���κ���ͼ��Ķ�������ΪC��1��0����ֱ��y=x+b��ö��κ�����ͼ����A��B���㣬���е�A������Ϊ��3��4������B��y���ϣ���PΪ�߶�AB�ϵ�һ�����㣨��P��A��B���غϣ�������P��x��Ĵ�����ö��κ�����ͼ���ڵ�E��
��ͼ����֪���κ���ͼ��Ķ�������ΪC��1��0����ֱ��y=x+b��ö��κ�����ͼ����A��B���㣬���е�A������Ϊ��3��4������B��y���ϣ���PΪ�߶�AB�ϵ�һ�����㣨��P��A��B���غϣ�������P��x��Ĵ�����ö��κ�����ͼ���ڵ�E���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
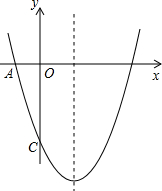 ��ͼ����֪���κ���y=ax2-4x+c��ͼ���������ύ�ڵ�A��-1��0���͵�C��0��-5����
��ͼ����֪���κ���y=ax2-4x+c��ͼ���������ύ�ڵ�A��-1��0���͵�C��0��-5�����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
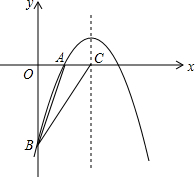 ��2012•��ˮһģ����ͼ����֪���κ���y=-
��2012•��ˮһģ����ͼ����֪���κ���y=-| 1 | 2 |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com